|
|
|
|
|
§ 10. Числовые неравенства и их свойства Числовые неравенства (окончание)731. Докажите неравенство:
732. (Для работы в парах.) Увеличится или уменьшится дробь 1) Рассмотрите на примерах, как изменяется дробь 2) Обсудите друг с другом ваши наблюдения и выскажите гипотезу для каждого случая. 3) Проведите доказательство: один — для случая а < b, а другой — для случая а > b. 4) Проверьте друг у друга правильность рассуждений. 733. Докажите, что при а > 0 верно неравенство
734. Докажите, что сумма любого положительного числа и числа, ему обратного, не меньше чем 2. 735. Докажите неравенство:
736. Используя выделение квадрата двучлена, докажите неравенство: а) а2 - 6а + 14 > 0; б) b2 + 70 > 16b. 737. Выберите из данных неравенств такое, которое не является верным при любом значении а.
738. (Для работы в парах.) Докажите, что если а и b — положительные числа и а2 > b2, то а > b. Пользуясь этим свойством, сравните числа:
1) Проведите доказательство приведённого утверждения.
739. Докажите, что при а ≥ 0 и b ≥ 0 верно неравенство
740. Что больше: а3 + b3 или аb(а + b), если а и b — неравные положительные числа? 741. К каждому из чисел 0, 1, 2, 3 прибавили одно и то же число k. Сравните произведение крайних членов получившейся последовательности чисел с произведением средних её членов. 742. Одноклассники Коля и Миша вышли одновременно из посёлка на станцию. Коля шёл со скоростью 5 км/ч, а Миша первую половину пути шёл со скоростью, на 0,5 км/ч большей, чем Коля, а вторую половину пути — со скоростью, на 0,5 км/ч меньшей, чем Коля. Кто из них первым пришёл на станцию? Упражнения для повторения743.Найдите значение дроби 744. Сократите дробь:
745. Решите уравнение:
Ответы739. Указание. Сравните квадраты левой и правой частей неравенства. 742. Коля. 743. 744. 745. а) 1; 5; б) 0,3; 2.
|
|
|



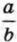 , где а и b — натуральные числа, если к её числителю и знаменателю прибавить по 1?
, где а и b — натуральные числа, если к её числителю и знаменателю прибавить по 1?
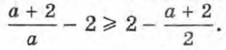
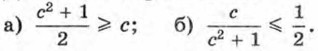
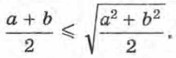
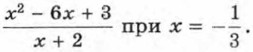

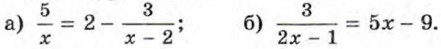
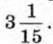
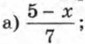 б) 1.
б) 1.