Погрешность и точность приближения

По графику функции у = х² нашли приближённые значения этой функции при х = 1,5 и х = 2,1:

если х = 1,5, то у ≈ 2,3;
если х = 2,1, то у ≈ 4,4.

По формуле у = х² можно найти точные значения этой функции:

если х = 1,5, то у = 1,5² = 2,25;
если х = 2,1, то у + 2,1² = 4,41.

Приближённое значение отличается от точного значения в первом случае на 0,05, а во втором на 0,01, так как:

2,3 - 2,25 = 0,05; 4,41-4,4 = 0,01.

Чтобы узнать, на сколько приближённое значение отличается от точного, надо из большего числа вычесть меньшее, т. е. найти модуль разности точного и приближённого значений. Этот модуль разности называют абсолютной погрешностью.

Определение. Абсолютной погрешностью приближённого значения называют модуль разности точного и приближённого значений.

Так, в рассмотренном примере абсолютная погрешность приближённого значения, равного 2,3, есть 0,05, а абсолютная погрешность приближённого значения, равного 4,4, есть 0,01:

|2,25 - 2,3| = |-0,05| = 0,05; |4,41 — 4,4| = 0,01.

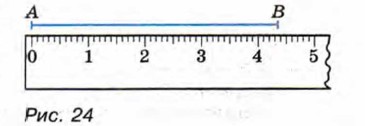
Найти абсолютную погрешность А не всегда возможно. Пусть, например, при измерении длины отрезка АВ, изображённого на рисунке 24, получен результат:

АВ ≈ 4,3 см.

Мы не можем найти абсолютную погрешность приближённого значения, так как не знаем точного значения длины отрезка АВ. В подобных случаях важно указать такое число, больше которого абсолютная погрешность быть не может. В рассматриваемом примере в качестве такого числа можно взять число 0,1. В самом деле, цена деления линейки 0,1 см, и поэтому абсолютная погрешность приближённого значения, равного 4,3, не больше чем 0,1, т. е.

|АВ - 4,3| ≤ 0,1.

Говорят, что число 4,3 есть приближённое значение длины отрезка АВ (в сантиметрах) с точностью до 0,1.

Вообще, если х ≈ а и абсолютная погрешность этого приближённого значения не превосходит некоторого числа h, то число а называют приближённым значением х с точностью до h. Пишут:

х ≈ а с точностью до h.

Используют также такую запись:

х = а ± h.

Запись х = а± h означает, что точное значение переменной х заключено между числами а - h и а + h, т. е.

a - h ≤ x ≤ a + h.

Например, на рулоне обоев написано, что его длина равна 18 ± 0,3 м. Значит, если l — истинное значение длины рулона (в метрах), то

18 - 0,3 ≤ l ≤ 18 + 0,3, т. е. 17,7 ≤ l ≤ 18,3.

Продолжение >>>