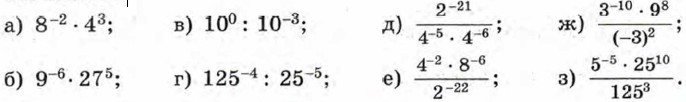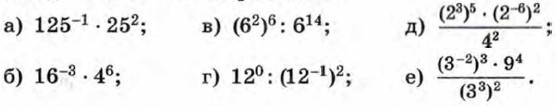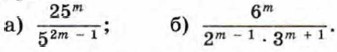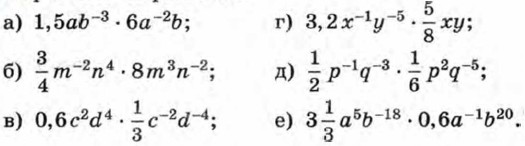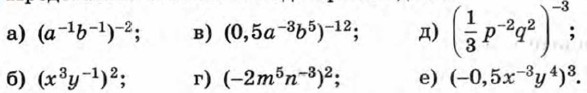|
|
|
|
|
§ 12. Степень с целым показателем и её свойства Свойства степени с целым показателем (продолжение)Упражнения985. Найдите значение выражения:
986. Вычислите:
987. Докажите, что степени любого отличного от нуля числа с противоположными показателями взаимно обратны. 988. Докажите, что 989. Вычислите:
990. Представьте выражение в виде степени с основанием 3 и найдите его значение: а) 27 • 3-4; б) (3-1)5 • 812; в) 9-2 : 3-6; г) 813 : (9-2)-3. 991. Представьте выражение в виде степени с основанием 2 и найдите его значение:
992. Представьте выражение, в котором m — целое число, в виде степени с основанием 5: а) 5m • 5m + 1 • 51- m; б) (5m)2 • (5-3)m; в) 625 : 54m - 2. 993. Вычислите:
994. Найдите значение выражения:
995. (Для работы в парах.) Зная, что m — целое число, сократите дробь:
1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.
996. Представьте какими-либо тремя способами выражение x-10 в виде произведения степеней. 997. Представьте выражение а12, где а ≠ 0, в виде степени: а) с основанием а4; б) с основанием а-6. 998. Представьте в виде степени с основанием х частное: a) x10 : x12;
999. Упростите выражение:
1000. Найдите значение выражения:
1001. Упростите выражение и найдите его значение:
1002. Представьте степень в виде произведения:
|
|
|



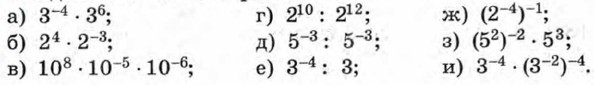
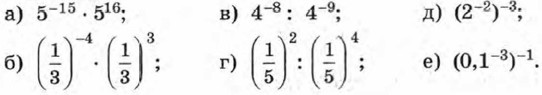
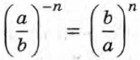 при любом целом n, а ≠ 0 и b ≠ 0.
при любом целом n, а ≠ 0 и b ≠ 0.
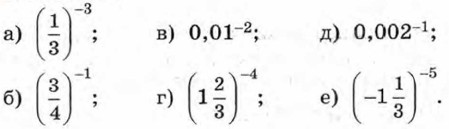
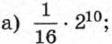 б) 32 • (2-4)2; в) 8-1 • 43; г) 45 • 16-2.
б) 32 • (2-4)2; в) 8-1 • 43; г) 45 • 16-2.