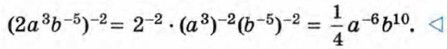|
|
|
|
|
§ 12. Степень с целым показателем и её свойства Свойства степени с целым показателемИзвестные вам свойства степени с натуральным показателем справедливы и для стеиеыи с любым целым показателем (пужно только предполагать, что основание степени не равно нулю).
Эти свойства можно доказать, опираясь на определение степени с целым отрицательным показателем и свойства степени с натуральным показателем. Докажем, например, справедливость свойства (1) (основного свойства степени) для случая, когда показатели степеней — целые отрицательные числа. Иначе говоря, докажем, что если k и р — натуральные числа и а ≠ 0, то а-k • а-р = а-k - р. Имеем
Заменяя степени а-k и а-р дробями Из свойств степени вытекает, что действия над степенями с целыми показателями выполняются по тем же правилам, что и действия над степенями с натуральными показателями. Пример 1. Преобразуем произведение а-17 • а21.
a-17 • a21 = a-17 + 21 = a4. Пример 2. Преобразуем частное b2 : b5.
b2 : b5 = b2 - 5 = b-3. Для степеней с натуральными и нулевым показателями мы могли применять правило деления степеней с одинаковыми основаниями в том случае, когда показатель степени делимого был не меньше показателя степени делителя. Теперь, после введения степеней с целыми показателями, это ограничение снимается: показатели степеней делимого и делителя могут быть любыми целыми числами. Пример 3. Упростим выражение (2а3b-5)-2.
|
|
|




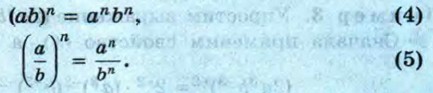
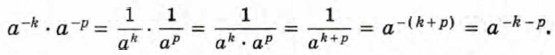
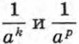 и дробь
и дробь 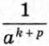 степенью а-(k + р), мы воспользовались определением степени с целым отрицательным показателем. Заменяя произведение аkар степенью аk + р, мы использовали основное свойство степени с натуральным показателем.
степенью а-(k + р), мы воспользовались определением степени с целым отрицательным показателем. Заменяя произведение аkар степенью аk + р, мы использовали основное свойство степени с натуральным показателем.
 При умножении степеней с одинаковыми основаниями основание оставляют тем же, а показатели степеней складывают. Имеем
При умножении степеней с одинаковыми основаниями основание оставляют тем же, а показатели степеней складывают. Имеем