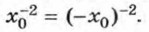|
|
|
|
|
Для тех, кто хочет знать больше Функции у = х-1 и у = х-2 и их свойства (продолжение)4. Значения аргумента и соответствующие им значения функции являются взаимно обратными числами. Действительно, при любых значениях аргумента х верно равенство ху = 1. А это означает, что значения х и у являются взаимно обратными числами. Если точка М (а; b) принадлежит графику данной функции, то точка М' (6; а) также принадлежит графику этой функции. Точки М (а; b) и М' (b; а) симметричны относительно прямой у = х. Значит, график функции у = х-1 симметричен относительно прямой у = х.
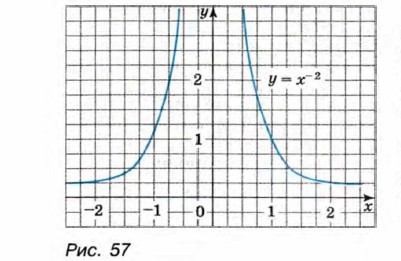
Выясним теперь свойства функции у = х-2 и особенности её графика. 1. При любом значении аргумента значения функции — положительные числа. Это следует из того, что х-2 > 0 при любом х ≠ 0. Значит, график функции у = х-2 расположен выше оси х. 2. Любым противоположным значениям аргумента соответствует одно и то же значение функции. Действительно, если х0 и -х0 — значения аргумента, то
Отсюда следует, что каждой точке М (x0; у0) графика функции соответствует точка М'(-х0; у0) того же графика. Значит, график функции у = х-2 симметричен относительно оси у. 3. Если х → +∞ или х → -∞, то у → 0; если х → 0, то у → +∞. Действительно, если |х| неограниченно возрастает (|x| → +∞), то | х-2| убывает, оставаясь положительным числом, т. е. у стремится к нулю. Если |x| → 0, то х-2 неограниченно возрастает, т. е. х-2 → +∞. Основываясь на этих свойствах, можно построить график функции у = х-2. Вычислим значения у для некоторых положительных значений аргумента.
Построим в координатной плоскости точки, координаты которых помещены в таблице. Соединив эти точки плавной непрерывной линией, получим одну ветвь графика функции. Вторую ветвь, расположенную во второй координатной четверти, построим симметрично первой относительно оси у. График функции у = х-2 изображён на рисунке 57.
|
|
|



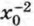 и (-х0)-2 — соответствующие им значения функции, но
и (-х0)-2 — соответствующие им значения функции, но