|
|
|
|
|
Для тех, кто хочет знать больше Функции у = х-1 и у = х-2 и их свойстваФункции, которые можно задать формулой вида у = хn, где х — независимая переменная и n — целое число, называют степенными функциями с целым показателем. Со степенными функциями у = х2 и у = х3 вы познакомились в курсе алгебры 7 класса. Вам знакома также степенная функция у = х, которая является частным случаем прямой пропорциональности у = kx (при k = 1). Рассмотрим теперь функции у = х-1 и у = х-2, выясним свойства этих функций и особенности их графиков. Отметим сразу, что областью определения каждой из этих функций является множество действительных чисел, кроме нуля. Перечислим свойства функции у = х-1 и особенности её графика. 1. Если х > 0, то у > 0; если х < 0, то у < 0. Это следует из формулы у = х-1: значения х и у одного знака. Так как
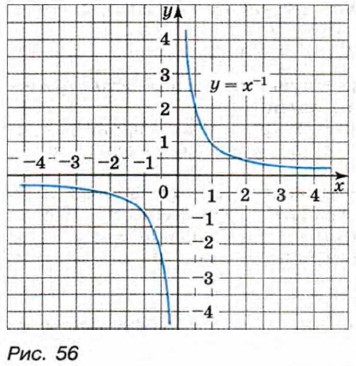
то графиком функции является гипербола, расположенная в первой и третьей четвертях координатной плоскости (рис. 56).
2. Противоположным значениям аргумента соответствуют противоположные значения функции. Действительно, если х0 и -х0 — значения аргумента, то соответствующие им значения функции
Если точка М (х0; у0) принадлежит графику функции, то точка М'(-х0; -у0) также принадлежит графику этой функции. Значит, каждой точке М (х0; у0) графика соответствует точка М'(-х0; -у0) того же графика. Точки, имеющие противоположные абсциссы и противоположные ординаты, симметричны относительно начала координат. Следовательно, график функции у = х-1 симметричен относительно начала координат. 3. Если значения аргумента при х > 0 неограниченно возрастают (х → +∞), то соответствующие им значения функции убывают, т. е. стремятся к нулю (у → 0). Если значения аргумента при х > 0 убывают, т. е. стремятся к нулю (х → 0), то соответствующие значения функции неограниченно возрастают (у → +∞). Если х < 0 и х → -∞, то у → 0.
Таким образом, точки графика, удаляясь от оси у вправо или влево, всё ближе приближаются к оси х, а удаляясь от оси х вверх или вниз, всё ближе приближаются к оси у. Отметим ещё одно свойство функции у = х-1.
|
|
|



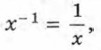
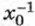 и (-x0)-1 также являются противоположными числами, так как
и (-x0)-1 также являются противоположными числами, так как
