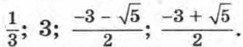|
|
|
|
|
§ 5. Уравнения с одной переменной Дробные рациональные уравнения (окончание)295. Найдите координаты точек пересечения графиков функций:
296. При каких значениях а: а) равны значения выражении б) являются противоположными числами значения выражений 297. Решите уравнение, используя введение новой переменной:
298. Найдите корни уравнения:
299. Решите уравнение:
300. Сумма данного положительного числа и числа, ему обратного, в 13 раз меньше суммы их кубов. Найдите это число. Повторение301. Сократите дробь:
302. Постройте график функции у = х2 - 3. Укажите промежутки, в которых функция принимает: а) положительные значения; б) отрицательные значения. 303. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила за 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде? Контрольные вопросы1. Какое уравнение с одной переменной называется целым? Приведите пример. 2. Как найти степень целого уравнения? 3. Дайте определение биквадратного уравнения. Объясните, как решают биквадратное уравнение. 4. Какое уравнение называется дробным рациональным? На примере уравнения Ответы288. а) 0; -3; б) 0; в) 0. 289. а) -√0,4; √0,4; б) 4. 290. а) 10; б) 0. 291. а) -1; 7; б) 2; 292. а) 1,5; б) -0,5 293. а) 8,2; 13; б) -6,6; 3. 294. а) 3,2; 8; б) 295. а) (-1; -9) (-3; -3), (3; 3). 296. а) -1,4; -0,5; 0,5; б) 297 а) -1; 3; б) -4; 3 в) -2; 4. 298. а) 1; 2,8; 6; б) 2; 5; 7 + 4√2; 7 - 4√2. 299. а) 300. 2 + √3; 2 - √3. 303. 24 дня и 12 дней
|
|
|



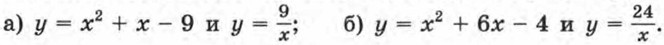
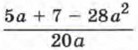 и а2;
и а2;
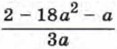 и 3а2?
и 3а2?
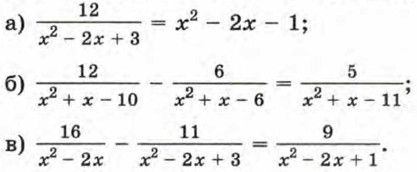
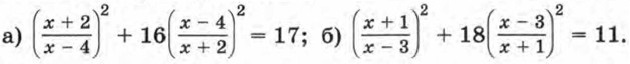
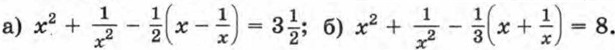
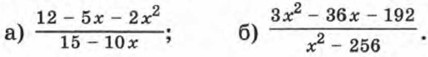
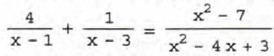 объясните, как решают дробные рациональные уравнения.
объясните, как решают дробные рациональные уравнения.
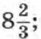 в) 4.
в) 4.
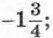 2.
2.
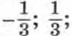 2.
2.
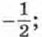 2;
2; 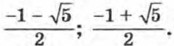 Указание. Введите новую переменную
Указание. Введите новую переменную 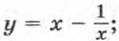 6)
6)