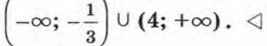|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств второй степени с одной переменнойНеравенства вида ах2 + bх + с > 0 и ах2 + bх + с < 0, где х — переменная, а, b и с — некоторые числа и а ≠ 0, называют неравенствами второй степени с одной переменной. Решение неравенства ах2 + bх + с > 0 или ах2 + bх + с < 0 можно рассматривать как нахождение промежутков, в которых функция у = ах2 + bх + с принимает положительные или отрицательные значения. Для этого достаточно проанализировать, как расположен график функции у = ах2 + bх + с в координатной плоскости: куда направлены ветви параболы — вверх или вниз, пересекает ли парабола ось х и если пересекает, то в каких точках. Рассмотрим примеры. Пример 1. Решим неравенство 5х2 + 9х - 2 < 0.
5х2 + 9х - 2 = 0. Это уравнение имеет два корня:
Значит, парабола пересекает ось х в двух точках, абсциссы которых равны -2 и Покажем схематически, как расположена парабола в координатной плоскости (рис. 51). Из рисунка видно, что функция принимает отрицательные значения, когда Заметим, что при рассмотренном способе решения неравенства нас не интересовала вершина параболы. Важно лишь было знать, куда направлены ветви параболы — вверх или вниз и каковы абсциссы точек ее пересечения с осью х. Пример 2. Решим неравенство 3х2 - 11x - 4 > 0.
Для того чтобы выяснить, пересекает ли парабола ось х и в каких точках, решим уравнение 3х2 - 11x - 4 = 0. Это уравнение имеет корни
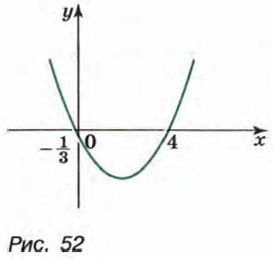
Покажем схематически, как расположена парабола в координатной плоскости (рис. 52). Из рисунка видно, что данное неравенство верно, если х принадлежит
промежутку или промежутку Ответ можно записать так:
|
|
|



 Рассмотрим функцию у = 5х2 + 9х - 2. Графиком этой функции является парабола, ветви которой направлены вверх. Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение
Рассмотрим функцию у = 5х2 + 9х - 2. Графиком этой функции является парабола, ветви которой направлены вверх. Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение
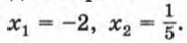
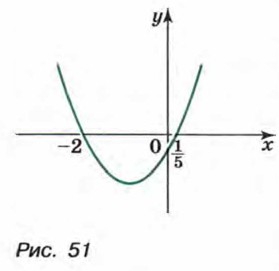
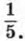
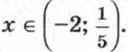 Следовательно, множеством решений неравенства 5х2 + 9x - 2 < 0 является числовой промежуток
Следовательно, множеством решений неравенства 5х2 + 9x - 2 < 0 является числовой промежуток 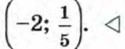
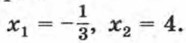
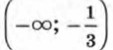 (4; +∞), т. е. множеством решений неравенства является объединение промежутков
(4; +∞), т. е. множеством решений неравенства является объединение промежутков