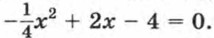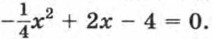|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств второй степени с одной переменной (продолжение)Пример 3. Решим неравенство
Ее графиком является парабола, ветви которой направлены вниз.
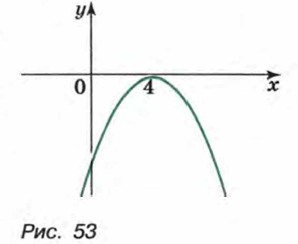
Выясним, как расположен график относительно оси х. Решим для этого уравнение Это уравнение имеет единственный корень х = 4. Значит, парабола касается оси х. Изобразив схематически параболу (рис. 53), найдем, что функция принимает отрицательные значения при любом х, кроме 4. Ответ можно записать так: х — любое число, не равное 4. Пример 4. Решим неравенство х2 - 3х + 4 > 0.
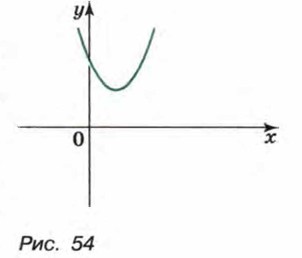
Чтобы выяснить, как расположена парабола относительно оси х, решим уравнение х2 - 3х + 4 = 0. Находим, что D = - 7 < 0, т. е. это уравнение не имеет корней. Значит, парабола не имеет общих точек с осью х. Показав схематически расположение параболы в координатной плоскости (рис. 54), найдем, что функция принимает положительные значения при любом х. Ответ: х — любое число. Итак, для решения неравенств вида ах2 + bх + с > 0 и ах2 + bх + с < 0 поступают следующим образом:
Упражнения304. Решите неравенство:
305. Найдите множество решений неравенства: а) 2x2 + 3х - 5 ≥ 0; б) -6x2 + 6х + 36 ≥ 0; в) -x2 + 5 ≤ 0. 306. Решите неравенство:
|
|
|



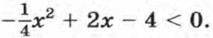
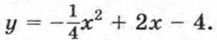
 Рассмотрим функцию
Рассмотрим функцию