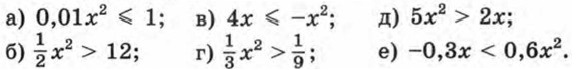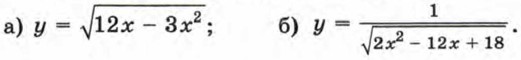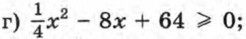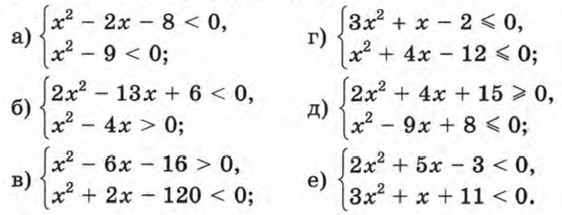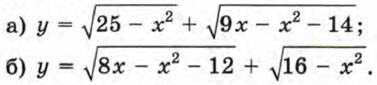|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств второй степени с одной переменной (окончание)307. Найдите, при каких значениях х трехчлен: а) 2x2 + 5х + 3 принимает положительные значения; б) 308. Решите неравенство:
309. Решите неравенство:
310. При каких значениях b уравнение имеет два корня: а) 3x2 + bх + 3 = 0; б) х2 + 2bх + 15 = 0? 311. При каких значениях t уравнение не имеет корней: а) 2х2 + tx + 18 = 0; б) 4х2 + 4tx + 9 = 0? 312. Найдите множество решений неравенства: а) 3х2 + 40x + 10 < -х2 + 11х + 3;
313. Решите неравенство: а) 2х(3х - 1) > 4х2 + 5х + 9;
314. Найдите область определения функции:
315. Докажите, что при любом значении переменной верно неравенство:
316. Какое из данных выражений принимает положительное значение при любом значении у?
317. Докажите, что: а) x2 + 7х + 1 > -x2 + 10x - 1 при любом х;
318. Одна сторона прямоугольника на 7 см больше другой. Какой может быть меньшая сторона, если площадь прямоугольника не превосходит 60 см2? 319. Длина прямоугольника на 5 см больше ширины. Какую ширину должен иметь прямоугольник, чтобы его площадь была больше 36 см2? 320. Решите систему неравенств:
321. Укажите все целые значения х, принадлежащие области определения функции:
|
|
|



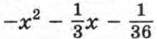 принимает отрицательные значения.
принимает отрицательные значения.