|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств методом интервалов (ответы)Упражнения для повторения339. Напишите уравнение прямой, которая: а) проходит через начало координат и точку А (0,6; -2,4);
340. Два сосуда были наполнены растворами соли, причем в первом сосуде содержалось на 1 л меньше раствора, чем во втором. Концентрация раствора в первом сосуде составляла 10%, а во втором — 20%. После того как растворы слили в третий сосуд, получили новый раствор, концентрация которого составила 16%. Сколько раствора было в каждом сосуде первоначально? Контрольные вопросы1. На примере неравенств 3х2 + 5х - 2 < 0 и х2 + 2х + 6 > 0 расскажите, как можно решить неравенство второй степени, используя свойства графика квадратичной функции. 2. На примере неравенства (х - 5)(х + 7)(х + 9) < 0 расскажите, как решают неравенства методом интервалов. Ответы325. а) (-∞; -8) ∪ (5; +∞); б) (-10; 14); в) (-∞; -8,5] ∪ [3,5; +∞); 326. а) (-25; 30); б) (-∞; -6) ∪ (6; +∞); 327. а) (2; 5) ∪ (12; +∞); б) (-∞; -7) ∪ (-1; 4); в) (-∞; -5) ∪ (-1; 0) ∪ (8; +∞). 328. а) (-48; 37) ∪ (42; +∞); б) (-∞; -0,7) ∪ (2,8; 9,2). 329. а) (-∞; -9) ∪ (2; 15) б) (-6; 0) ∪ (5; +∞); в) (1; 4) ∪ (8; 16). 330. 331. а) (-∞; 18) ∪ (19; +∞); б) (-∞; -0,9) ∪ (3,2; +∞); в) [-3; 8,5); г) [0,3; 8]. 332. а) [-8; 5]; б) [-12; 1] ∪ [9; +∞) 333. а) (-∞; -2,5] ∪ [17; +∞); б) [-9; 0] ∪ [4; +∞). 334. а) (-6; 5) б) (-; -3,8) ∪ (1,4; +∞); в) (—∞; 0) ∪ (1,6; +∞); г) (-∞; 0,3) ∪ (4; +∞) 335. а) (-7; 21); б) (-∞; -4,7) ∪ (7,2; +∞); 336. а) (-∞; 1] ∪ (3; +∞); б) [-6; 5); в) (0; 2]; г) (-∞; 1) ∪ [1,5; +∞). 337. а) (-16; -4); б) (-∞; 2) ∪ (2,5; +∞); в) (-∞; 0) ∪ (0,5; +∞); г) (-4; -1,2). 338. а) (-4; 0); б) (-∞; -1) ∪ (0; +∞); в) (1; 2]; г) (-∞; -2) ∪ [1,5; +∞). 339. а) у = -4х; б) у = 1,6х + 4. 340. 2 л и 3 л.
|
|
|



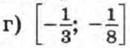
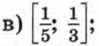 г) (-∞; -6,3] ∪ [-0,1; +∞]
г) (-∞; -6,3] ∪ [-0,1; +∞]
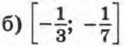 в) (-12; 3)
в) (-12; 3) 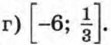
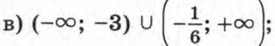 г) (0; 3).
г) (0; 3).