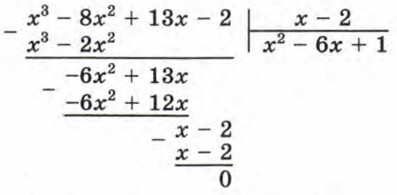|
|
|
|
|
Для тех, кто хочет знать больше Приемы решения целых уравненийМы уже отмечали, что формулы корней целых уравнений третьей и четвертой степеней с одной переменной громоздки и неудобны для практического использования, а для уравнений пятой и более высоких степеней формул корней вообще не существует. Такие уравнения удается иногда решить, используя специальные приемы.
Если число а является корнем многочлена Р(х) = а0хn + a1xn-1 + ... + аn-1х + аn, где а0 ≠ 0, то этот многочлен можно представить в виде произведения (х - а) Р1(х), где Р1(х) — многочлен n - 1-й степени.
Если уравнение а0хn + а1хn - 1 + ... + аn - 1х + аn = 0, в котором все коэффициенты — целые числа, причем свободный член отличен от нуля, имеет целый корень, то этот корень является делителем свободного члена.
Отсюда
Число, записанное в этом равенстве в скобках, является целым, так как х0 и все коэффициенты -а0, -а1, ..., -аn - 1 — целые числа. Значит, при делении аn на х0 получается целое число, т. е. х0 — делитель свободного члена. Приведем примеры решения целых уравнений с использованием указанных теорем. Один из приемов решения уравнения вида Р(х) = 0, где Р(х) — многочлен третьей или более высокой степени, состоит, как известно, в разложении многочлена Р(х) на множители. Пример 1. Решим уравнение х3 - 8х2 + 13х - 2 = 0.
Для того чтобы найти многочлен Р(х), разделим многочлен х3 - 8х2 + 13х - 2 на двучлен х - 2. Деление многочленов выполним «уголком»:
Значит, исходное уравнение можно представить в виде (х - 2) (х2 — 6х + 1) = 0. Отсюда х - 2 = 0 или х2 - 6х + 1 = 0. Первое уравнение имеет единственный корень — число 2. Второе уравнение имеет два корня: 3 - √8 и 3 + √8. Исходное уравнение имеет три корня: 2, 3 - √8, 3 + √8. Еще один прием, который используется при решении целых уравнений третьей и более высоких степеней, состоит, как вы знаете, во введении новой переменной.
|
|
|



 Пусть х0 — целый корень данного уравнения. Тогда верно равенство
Пусть х0 — целый корень данного уравнения. Тогда верно равенство
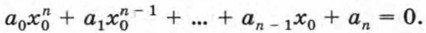
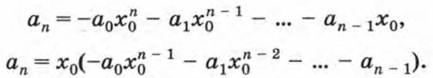

 Если это уравнение имеет целый корень, то в силу теоремы 2 он является делителем числа -2, т. е. равен одному из чисел 1, -1, 2, -2. Проверка убеждает нас, что корнем уравнения является число 2. Значит, в силу теоремы 1 многочлен х3 - 8х2 + 13х - 2 можно представить в виде (х - 2) F(x), где F(х) — многочлен второй степени.
Если это уравнение имеет целый корень, то в силу теоремы 2 он является делителем числа -2, т. е. равен одному из чисел 1, -1, 2, -2. Проверка убеждает нас, что корнем уравнения является число 2. Значит, в силу теоремы 1 многочлен х3 - 8х2 + 13х - 2 можно представить в виде (х - 2) F(x), где F(х) — многочлен второй степени.