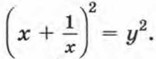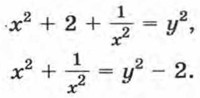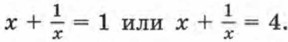|
|
|
|
|
Для тех, кто хочет знать больше Приемы решения целых уравнений (продолжение)Пример 2. Решим уравнение 2007 (х4 - 6х2 + 9) + 2006(х2 - 3) - 1 = 0.
2007y2 + 2006y -1 = 0. Применение формулы корней квадратного уравнения приводит здесь к громоздким вычислениям. Поступим иначе. Попытаемся найти целый корень уравнения, если он существует. По теореме 2 он является делителем числа -1, т. е. равен 1 или -1. Подставляя в уравнение числа 1 и -1, убеждаемся, что корнем уравнения является число -1. Второй корень квадратного уравнения найдем, используя теорему Виета. Так как Из равенств
найдем корни исходного уравнения:
Метод введения новой переменной находит применение при решении возвратных уравнений. Возвратным уравнением называется уравнение вида а0хn + а1хn - 1 + ... + аn - 1х + аn = 0, в котором коэффициенты членов уравнения, одинаково отстоящих от начала и конца, равны, т. е. аk = аn - k, где k = 0, 1, 2, ..., n. Рассмотрим пример решения возвратного уравнения четвертой степени. Пример 3. Решим уравнение х4 - 5х3 + 6х2 - 5х + 1 = 0.
Разделив обе части уравнения на х2, получим равносильное ему уравнение
Сгруппируем первый член с последним и второй с четвертым, причем во второй сумме вынесем множитель -5 за скобки. Получим
Введем новую переменную:
Отсюда
Выполнив подстановку, получим (у2 - 2) - 5у + 6 = 0,
Полученное квадратное уравнение имеет два корня: у1 = 1 и y2 = 4. Значит,
Решая эти уравнения, найдем, что первое из них не имеет корней, а второе имеет два корня: x1 = 2- √3 и х2 = 2 + √3. Значит, исходное возвратное уравнение имеет два корня: 2 - √3 и 2 + √3. Иногда удается решить целое уравнение, воспользовавшись свойством возрастания или убывания функций.
|
|
|



 Используем подстановку у = х2 - 3. Получим квадратное уравнение
Используем подстановку у = х2 - 3. Получим квадратное уравнение
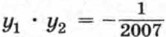 и
и 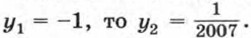
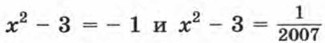
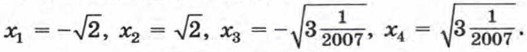
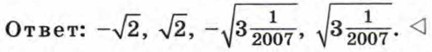
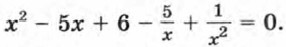
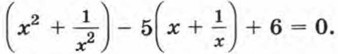
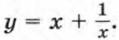 Тогда
Тогда