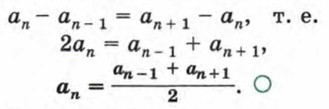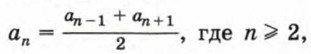Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии(продолжение)

Пример 1. Последовательность (с_n) — арифметическая прогрессия, в которой с₁ = 0,62 и d = 0,24. Найдем пятидесятый член этой прогрессии.

Имеем

с₅₀ = 0,62 + 0,24 • (50 - 1) = 12,38.

Пример 2. Выясним, является ли число -122 членом арифметической прогрессии (x_n):

23; 17,2; 11,4; 5,6; ... .

В данной арифметической прогрессии х₁ = 23 и d = х₂ - х₁ = 17,2 - 23 = -5,8. Запишем формулу л-го члена прогрессии:

х_n = 23 - 5,8 (_n - 1), т. е.
х_n = 28,8 - 5,8n.

Число -122 является членом арифметической прогрессии (х_n), если существует такое натуральное число n, при котором значение выражения 28,8 - 5,8n равно -122.

Решим уравнение 28,8 - 5,8n = -122:

5,8n = 150,8, n = 26.

Отметим важное свойство арифметической прогрессии:

каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов.

Действительно, если последовательность (а_n) является арифметической прогрессией, то

если в последовательности (а_n) каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.

Действительно, из равенства

следует, что

2а_n = a_{n - 1} + а_n+1,
a_n - а_{n - 1} = а_{n + 1} - а_n,

а это означает, что разность между последующим и предыдущим членами последовательности (а_n) остается постоянной. Значит, последовательность (а_n) — арифметическая прогрессия.

Заметим, что формулу n-го члена арифметической прогрессии а_n = а₁ + d(n- 1) можно записать иначе:

а_n = dn + (а₁ - d).

Отсюда ясно, что

любая арифметическая прогрессия может быть задана формулой вида

а_n = kn + b,

где k и b — некоторые числа.

Верно и обратное:

последовательность (а„), заданная формулой вида

а_n = kn + b,

где k и b — некоторые числа, является арифметической прогрессией.

Действительно, найдем разность (n + 1)-го и n-го членов последовательности (а_n):

а_{n + 1} - а_n = k(n + 1) + b - (kn + b) = kn + k + b - kn - b = k.

Значит, при любом л справедливо равенство а_{n + 1} = а_n + А, и по определению последовательность (а_n) является арифметической прогрессией, причем разность этой прогрессии равна k.

<<< К началу Окончание >>>