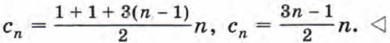|
|
|
|
|
§ 9. Арифметическая прогрессия Формула суммы первых n членов арифметической прогрессии (продолжение)Пример 2. Найдем сумму первых сорока членов последовательности (аn), заданной формулой аn = 5n - 4.
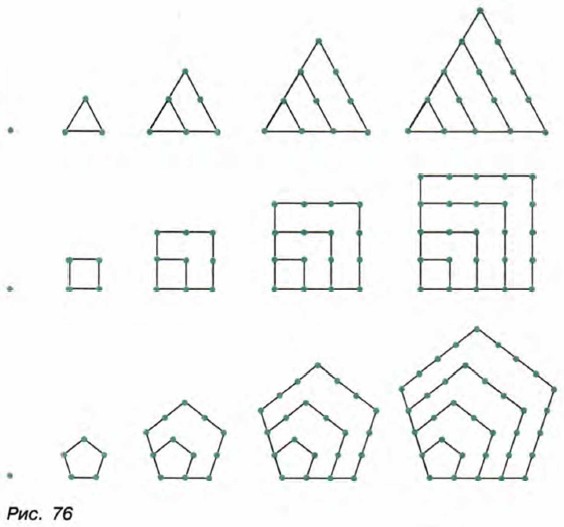
Теперь по формуле (I) вычислим S40: Пример 3. Найдем сумму всех натуральных чисел, кратных шести и не превосходящих 250.
Имеем
Пример 4. Пифагор (IV в. до н. э.) и его ученики рассматривали последовательности, связанные с геометрическими фигурами. Подсчитывая число кружков в треугольниках, квадратах, пятиугольниках (рис. 76), они получали: — последовательность (аn) треугольных чисел 1, 3, 6, 10, 15, ... ; — последовательность (bn) квадратных чисел 1, 4, 9, 16, 25, ... ; — последовательность (сn) пятиугольных чисел 1, 5, 12, 22, 35, ... .
Зададим каждую из этих последовательностей формулой л-го члена.
ДИОФАНТ (III в.) — древнегреческий математик из Александрии. В его «Арифметике» изложены начала алгебры, решен ряд задач, сводящихся к неопределенным уравнениям различных степеней. Теория диофантовых уравнений и теория диофантовых приближений — так названы два больших раздела современной теории чисел. Его труды оказали большое влияние на развитие математики.
a1 = 1, а2 = 1 + 2, а3 = 1 + 2 + 3, аn = 1 + 2 + 3 + ... + n. Значит, Последовательность (bn) квадратных чисел аналогичным способом получается из последовательности нечетных чисел 1, 3, 5, ... , т. е. из арифметической прогрессии, первый член которой равен 1 и разность равна 2: b1 = 1, b2 = 1 + 3, b3 = 1 + 3 + 5,
Следовательно, Последовательность (сn) пятиугольных чисел таким же способом можно получить из арифметической прогрессии 1, 4, 7, ... , в которой первый член равен 1 и разность равна 3: с1 = 1, с2 = 1 + 4, с3 = 1 + 4 + 7,
Значит,
|
|
|



 Последовательность (аn) является арифметической прогрессией, так как она задана формулой вида аn = kn + b, где k = 5 и b = -4. Найдем первый и сороковой члены этой арифметической прогрессии: а1 = 5 • 1 — 4 = 1, а40 = 5 • 40 - 4 = 196.
Последовательность (аn) является арифметической прогрессией, так как она задана формулой вида аn = kn + b, где k = 5 и b = -4. Найдем первый и сороковой члены этой арифметической прогрессии: а1 = 5 • 1 — 4 = 1, а40 = 5 • 40 - 4 = 196.
 Значит, число членов прогрессии, сумму которых надо найти, равно 41.
Значит, число членов прогрессии, сумму которых надо найти, равно 41.
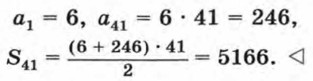

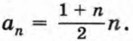
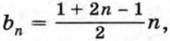 bn = n2. Мы пришли к формуле, очевидной для последовательности квадратных чисел.
bn = n2. Мы пришли к формуле, очевидной для последовательности квадратных чисел.