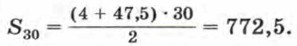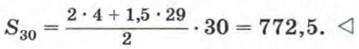|
|
|
|
|
§ 9. Арифметическая прогрессия Формула суммы первых n членов арифметической прогрессииПусть требуется найти сумму первых ста натуральных чисел. Покажем, как можно решить эту задачу, не выполняя непосредственного сложения чисел. Обозначим искомую сумму через S и запишем ее дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором — в порядке убывания: S = 1 + 2 + 3 + ... + 98 + 99 + 100,
Каждая пара чисел, расположенных друг под другом, дает в сумме 101. Всего таких пар 100. Поэтому, сложив равенства почленно, получим
Итак, 1 + 2 + 3 + ... + 99 + 100 = 5050. С рассмотренной задачей связана история, которую рассказывают об известном немецком математике Карле Гауссе. Когда учитель предложил ученикам третьего класса сложить все числа от 1 до 100 включительно, рассчитывая при этом надолго занять их работой, маленький Карл моментально подошел с готовым ответом. Возможно, он заметил, что каждая из сумм 1 + 100, 2 + 99, 3 + 98, ... равна 101, а таких сумм 50. С помощью рассуждений, аналогичных тем, которые мы провели при вычислении суммы первых ста натуральных чисел, можно найти сумму первых n членов любой арифметической прогрессии. Обозначим сумму первых n членов арифметической прогрессии (аn) через Sn и запишем эту сумму дважды, расположив в первом случае слагаемые в порядке возрастания их номеров, а во втором случае в порядке убывания: Sn = а1 + a2 + a3 + a4 + ... + an - 1 + an, (1)
Сумма каждой пары членов прогрессии, расположенных друг под другом, равна а1 + аn. Действительно, а2 + аn - 1 = (a1 + d) + (an - d) = а1 + аn,
Число таких пар равно n. Поэтому, сложив почленно равенства (1) и (2), получим 2Sn = (а1 + аn)n. Разделив обе части последнего равенства на 2, получим формулу суммы первых n членов арифметической прогрессии:
Т. е.
Приведем примеры на вычисление суммы членов арифметической прогрессии. Пример 1. Найдем сумму первых тридцати членов арифметической прогрессии 4; 5,5; ... .
Тридцатый член прогрессии найдем по формуле n-го члена: а30 = 4 + 1,5 • 29 = 47,5. Теперь вычислим сумму первых тридцати членов, воспользовавшись формулой (I):
Если для решения рассмотренной задачи воспользоваться формулой (II), то вычисления будут выглядеть так:
КАРЛ ГАУСС (1777—1855) — немецкий математик, астроном, геодезист, физик. Выдающиеся математические способности проявил в раннем детстве. Его многочисленные исследования в области алгебры, теории чисел, геометрии и математического анализа оказали значительное влияние на развитие теоретической и прикладной математики, астрономии, геодезии, физики.
|
|
|



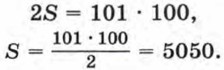

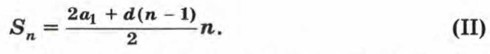
 В данной арифметической прогрессии а1 = 4, d = 1,5.
В данной арифметической прогрессии а1 = 4, d = 1,5.