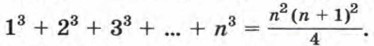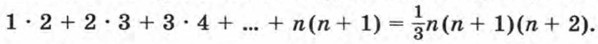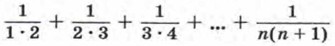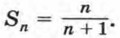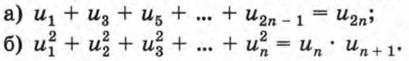Метод математической индукции (окончание)

Пример 2. Докажем, что при любом натуральном n сумма 13ⁿ + 5 кратна 6.

При n = 1 утверждение верно, так как 131 + 5 = 18, а число 18 кратно 6.

Допустим, что утверждение верно при n = k, т. е. сумма 13^k + 5 кратна 6, и докажем, что из этого следует его справедливость для n = k + 1, т. е. сумма 13^{k + 1} + 5 также кратна 6.

Имеем

13^{k + 1} + 5 = 13^k • 13 + 5 = 13^k(12 + 1) + 5 = 13^k • 12 + (13^k + 5).

В полученной сумме каждое слагаемое кратно 6. Значит, сумма 13^{k + 1} + 5 при любом натуральном k кратна 6. В силу принципа математической индукции утверждение доказано.

Упражнения

662. Проверьте, что при n = 1, 2, 3 верна формула

Докажите, что эта формула верна при любом натуральном n.

663. Докажите, что при любом натуральном n верно равенство

664. Докажите, что при любом натуральном n сумма

может быть вычислена по формуле

665. Докажите, что при любом натуральном n верно равенство

1 • 4 + 2 • 7 + 3 • 10 + ... + n (3n + 1) = n (n + 1)².

666. Пусть (b_n) — последовательность, в которой b₁ = -3, b_{k + 1} = b_k + 6k + 3. Докажите, что эту последовательность можно задать формулой b_n = 3n² - 6.

667. Докажите, что последовательность (а_n), в которой а₁ = -5, а_{k + 1} = а_k + 10k + 5, можно задать формулой а_n = 5n² - 10.

668. Докажите, что разность 49ⁿ - 1 кратна 48 при любом натуральном n.

669. Пусть (u_n) — последовательность чисел Фибоначчи, т. е. u₁ = 1, u₂ = 1, u_{n + 2} = u_n + u_{n + 1} при n > 2. Докажите, что эта последовательность обладает следующим свойством:

<<< К началу