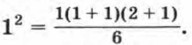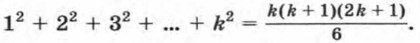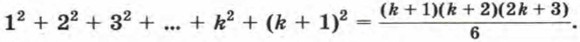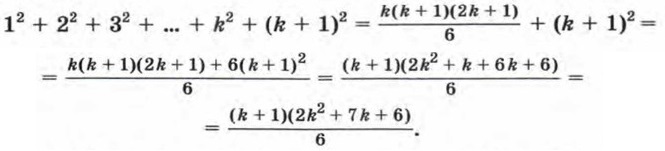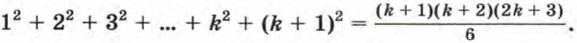|
|
|
|
|
Для тех, кто хочет знать больше Метод математической индукцииПусть дана последовательность (аn), в которой а1 = 4, аn+1 = аn + 2n+ 3. Попытаемся задать ее формулой n-го члена. Вычислим первые несколько членов последовательности: а1 = 4, а2 = 4 + 2 • 1 + 3 = 9, а3 = 9 + 2 • 2 + 3 = 16. Значит, последовательность (аn) начинается так: 4, 9, 16, ... . Естественно предположить, что эту последовательность можно задать формулой аn = (n + 1)2. Формула верна для n = 1, 2, 3. Однако, как долго ни продолжали бы мы вычисления, они не дают оснований утверждать, что эта формула верна при любом натуральном n. Поэтому воспользуемся специальным методом рассуждений. Предположим, что формула верна при n = k, т. е. аk = (k + 1)2, и докажем, что она также верна при n = k + 1, т. е. докажем, что an + 1 = (k + 2)2. По условию ак+1 = аk + 2k + 3. Заменив аk на (k + 1)2, получим ak+ 1 = (k + 1)2 + 2k + 3 = k2 + 2k + 1 + 2k + 3 = k2 + 4k + 4 = (k + 2)2. Значит, ak + 1 = (k + 2)2, т. е. если формула верна для n = k, то она верна и для n = k + 1. Мы убедились, что формула верна для n = 1. Следовательно, она верна и для n = 1 + 1, т. е. для n = 2. Из того, что формула верна для n = 2, следует, что она верна и для n = 2 + 1, т. е. для n = 3. (Заметим, что в справедливости формулы для n = 2 и n = 3 нас убедили и непосредственные расчеты.) Из справедливости формулы для n = 3 вытекает ее справедливость для n = 3 + 1, т. е. для n = 4. Из того, что формула верна для n = 4, следует, что она верна для n = 5 и т. д. Ясно, что, строя такую цепочку рассуждений, мы дойдем до любого натурального числа. Значит, формула аn = (n + 1)2 верна при любом натуральном n, т. е. последовательность (аn) можно задать этой формулой. Примененный метод доказательства называется методом математической индукции. Он основан на следующем положении, известном под названием принцип математической индукции:
Доказательство некоторого утверждения методом математической индукции состоит из двух частей. Сначала проверяют его справедливость при n = 1. Затем, предположив, что утверждение верно при n = k, доказывают, что оно верно и при n = k + 1. Рассмотрим примеры применения метода математической индукции. Пример 1. При решении некоторых задач из геометрии и механики Архимед (287—212 гг. до н. э.) вывел формулу
Докажем ее справедливость.
Допустим, что эта формула верна для n = k, т. е.
Докажем, что отсюда следует ее справедливость для n = k + 1, т. е.
Имеем
Разложив на множители квадратный трехчлен 2k2 + 7k+ 6, получим 2k2 + 7k + 6 = (k + 2)(2k + 3). Значит,
Таким образом, справедливость формулы Архимеда доказана.
|
|
|



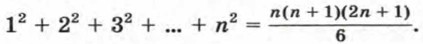
 При n = 1 формула верна:
При n = 1 формула верна: