|
|
|
|
|
§ 12. Начальные сведения из теории вероятностей Относительная частота случайного событияВ повседневной жизни, в практической и научной деятельности часто наблюдают те или иные явления, проводят определенные эксперименты. В процессе наблюдения или эксперимента приходится встречаться с некоторыми случайными событиями, т. е. такими событиями, которые могут произойти или не произойти. Например, выпадение орла или решки при подбрасывании монеты, поражение мишени или промах при выстреле, выигрыш спортивной команды во встрече с соперником, проигрыш или ничейный результат — все это случайные события. Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей. Методы теории вероятностей применяются в информатике, физике, астрономии, биологии, медицине и во многих других областях знаний.
ЯКОБ БЕРНУЛЛИ (1654—1705) — швейцарский ученый, занимавшийся различными вопросами математики и ее приложениями. Он впервые доказал теорему, устанавливающую связь между вероятностью события и частотой его появления («закон больших чисел»), имеющую важное значение в теории вероятностей и ее приложении. Зарождение теории вероятностей произошло в поисках ответа на вопрос: как часто наступает то или иное событие в большой серии происходящих в одинаковых условиях испытаний со случайными исходами?
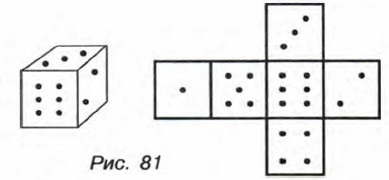
Рассмотрим пример. Провели такие испытания. Бросали 100 раз игральный кубик, т. е. небольшой куб, на гранях которого выбиты очки от одного до шести (рис. 81), и наблюдали, сколько раз на верхней грани кубика выпадет шесть очков. При бросании игрального кубика на его верхней грани может выпасть одно, два, три, четыре, пять или шесть очков. Каждое из этих шести событий, или, как говорят, шести исходов испытания, является случайным. Допустим, что в данной серии экспериментов «шестерка» выпала 17 раз. Число 17, которое показывает, сколько раз в этом испытании произошло рассматриваемое событие, называют частотой этого события, а отношение частоты к общему числу испытаний, равное Вообще пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло или нет интересующее нас событие А. Обозначим буквой n общее число испытаний, а буквой m число испытаний, при которых произошло событие А. Число т называют частотой события А, а отношение
АНДРЕЙ НИКОЛАЕВИЧ КОЛМОГОРОВ (1903-1987)— русский математик, работы которого относятся ко многим разделам математики и ее приложений — математическому анализу, теории вероятностей, топологии, механике, теории дифференциальных уравнений. Им построена современная система аксиоматического обоснования теории вероятностей, проведены исследования по статистическим методам контроля массовой продукции.
|
|
|




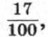 называют относительной частотой этого события.
называют относительной частотой этого события.
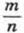 — относительной частотой.
— относительной частотой.
