|
|
|
|
|
Для тех, кто хочет знать больше Сложение и умножение вероятностей (окончание)Пример 3. В непрозрачном пакете лежат 9 жетонов с номерами 1, 2, ..., 9. Из пакета наугад вынимают один жетон, записывают его номер и жетон возвращают в пакет. Затем опять вынимают жетон и записывают его номер. Какова вероятность того, что оба раза будут вынуты жетоны, номера которых являются простыми числами?
Заметим, что если бы после первого извлечения жетон не возвращался обратно, то события А и В были бы зависимыми. Действительно, после первого извлечения жетона в пакете осталось бы 8 жетонов. Если в первый раз извлекли жетон, номер которого простое число, Пример 4. В результате многократных наблюдений установили, что вероятность попадания в мишень одного стрелка равна 0,9, а другого — 0,8. Каждый из стрелков сделал по одному выстрелу по мишени. Какова вероятность того, что мишень будет поражена?
А — первый стрелок попал в мишень;
События А и В независимые. Однако воспользоваться в этом случае умножением вероятностей нельзя, так как событие С наступает не только тогда, когда оба стрелка попали в мишень, но и тогда, когда в мишень попал хотя бы один из них. Поступим иначе. Рассмотрим события Р( Из свойства вероятностей противоположных событий вытекает, что Р( Отсюда получаем, что Р( Так как события С и Р(С) = 1 - Р( Значит, вероятность того, что мишень будет поражена, равна 0,98.
|
|
|



 Пусть событие А состоит в том, что в первый раз вынут жетон, номер которого является простым числом, а событие В — в том, что во второй раз вынут жетон, номер которого является простым числом. Тогда
Пусть событие А состоит в том, что в первый раз вынут жетон, номер которого является простым числом, а событие В — в том, что во второй раз вынут жетон, номер которого является простым числом. Тогда 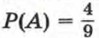 и
и 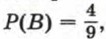 так как из чисел 1, 2, ..., 9 четыре числа являются простыми. Рассмотрим событие С, которое состоит в том, что оба раза вынуты жетоны, номера которых являются простыми числами. Событие В не зависит от события А, так как на повторное извлечение жетона не влияет то, какой жетон был вынут в первый раз (извлеченный в первый раз жетон был возвращен в пакет). Значит,
так как из чисел 1, 2, ..., 9 четыре числа являются простыми. Рассмотрим событие С, которое состоит в том, что оба раза вынуты жетоны, номера которых являются простыми числами. Событие В не зависит от события А, так как на повторное извлечение жетона не влияет то, какой жетон был вынут в первый раз (извлеченный в первый раз жетон был возвращен в пакет). Значит,
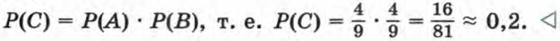
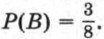 Если же в первый раз извлекли жетон, номер которого не простое число, то
Если же в первый раз извлекли жетон, номер которого не простое число, то 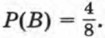
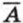 ,
, 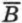 и
и 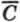 , противо; положные соответственно событиям А, В и С. События
, противо; положные соответственно событиям А, В и С. События 