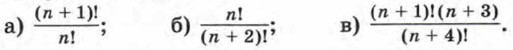Дополнительные упражнения к параграфу 11

831. Сколько существует четырехзначных чисел, кратных 10, если цифры в числах могут повторяться?

832. Пешеход должен пройти один квартал на север и три квартала на запад. Выпишите все возможные маршруты пешехода.

833. Выпишите все пятизначные числа, записанные тремя четверками и двумя единицами.

834. Из цифр 1, 2, 3, 5 составили все возможные четырехзначные числа (без повторения цифр). Сколько среди них таких чисел, которые больше 2000, но меньше 5000?

835. Сколько четных четырехзначных чисел, в которых цифры не повторяются, можно записать с помощью цифр:

а) 1, 2, 3, 7; б) 1, 2, 3, 4?

836. Делится ли число 50! на:

а) 100; б) 305; в) 1550?

837. Найдите наименьшее значение n, при котором число n! оканчивается:

а) одним нулем; б) двумя нулями; в) тремя нулями.

838. Из цифр 1, 2, 3, 4, 5 составили все возможные трехзначные числа (без повторения цифр). Сколько среди них таких, которые:

а) кратны 2; б) кратны 3?

839. Сократите дробь:

841. Сколькими способами из класса, где учатся 24 учащихся, можно выбрать:

а) двух дежурных; б) старосту и помощника старосты?

842. У Антона шесть друзей. Он может пригласить в гости одного или нескольких из них. Определите общее число возможных вариантов.

843. Сколько команд участвовало в финале первенства, если известно, что каждая команда сыграла с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника, причем всего было сыграно 30 игр?

844. Сколькими способами четыре пассажира: Алексеев, Смирнов, Федоров и Харитонов — могут разместиться в девяти вагонах поезда, если:

а) все они хотят ехать в разных вагонах;
б) Алексеев и Смирнов хотят ехать в одном вагоне, а Федоров и Харитонов — в других вагонах, причем различных?

845. На плоскости отметили несколько точек, никакие три из них не лежат на одной прямой. Через каждые две точки провели прямую. Сколько точек было отмечено, если всего было проведено 28 прямых?

846. В 9 «А» классе учатся 25 учащихся, в 9 «Б» — 20 учащихся, а в 9 «В» — 18 учащихся. Для работы на пришкольном участке надо выделить трех учащихся из 9 «А», двух — из 9 «Б» и одного — из 9 «В». Сколько существует способов выбора учащихся для работы на пришкольном участке?

847. Из группы туристов требуется выбрать дежурного и его помощника. Если бы туристов было на одного больше, то возможностей выбора было бы в 1,25 раза больше. Сколько туристов в группе?

848. Сколькими способами группу из 12 человек можно разбить на две группы:

а) по 4 и 8 человек; б) по 5 и 7 человек?

849. В отделе работают 5 ведущих и 8 старших научных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в командировку?

Ответы >>>