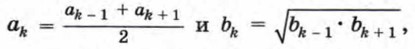|
|
|
|
|
Исторические сведения О прогрессияхПервые представления об арифметической и геометрической прогрессиях были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания, как их решать. В древнеегипетском папирусе Ахмеса (ок. 2000 г. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялась В этой задаче речь идет об арифметической прогрессии. Условие задачи, пользуясь современными обозначениями, можно записать так: S10 = 10, В одном древнегреческом папирусе приводится задача: «Имеется 7 домов, в каждом по 7 кошек, каждая кошка съедает 7 мы шей, каждая мышь съедает 7 колосьев, каждый из которых, если посеять зерно, дает 7 мер зерна. Нужно подсчитать сумму числа домов, кошек, мышей, колосьев и мер зерна». Решение этой задачи приводит к сумме: 7 + 72 + 73 + 74 + 75, т. е. сумме пяти членов геометрической прогрессии. О прогрессиях и их суммах знали древнегреческие ученые. Так, им были известны формулы суммы первых п чисел последовательности натуральных, четных и нечетных чисел. Архимед (III в. до н. э.) для нахождения площадей и объемов фигур применял «атомистический метод», для чего ему потребовалось находить суммы членов некоторых последовательностей. Он вывел формулу суммы квадратов натуральных чисел
показал, как найти сумму бесконечной убывающей геометрической прогрессии
Отдельные факты об арифметической и геометрической прогрессиях знали китайские и индийские ученые. Об этом говорит, например, известная индийская легенда об изобретателе шахмат (см. с. 157). Термин «прогрессия» (от латинского progressio, что означает «движение вперед») был введен римским автором Боэцием (VI в.) и понимался в более широком смысле, как бесконечная числовая последовательность. Названия «арифметическая» и «геометрическая» были перенесены на прогрессии из теории непрерывных пропорций, изучением которых занимались древние греки. Равенство вида аk - 1 - аk = аk - аk + 1 они называли непрерывной арифметической пропорцией, а равенство
т. е. этими соотношениями выражаются характеристические свойства арифметической и геометрической прогрессий. Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (III в.). Формула суммы членов геометрической прогрессии дана в книге Евклида «Начала» (III в. до н. э.). Правило отыскания суммы членов произвольной арифметической прогрессии встречается в «Книге абака» Л. Фибоначчи (1202). Общее правило для суммирования любой бесконечной убывающей геометрической прогрессии дает Н. Шюке в книге «Наука о числах» (1484).
|
|
|



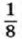 меры».
меры».
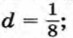 найти а1, а2, ..., а10.
найти а1, а2, ..., а10.
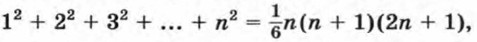
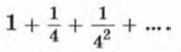
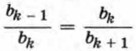 — непрерывной геометрической пропорцией. Из этих равенств следует, что
— непрерывной геометрической пропорцией. Из этих равенств следует, что