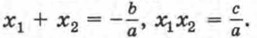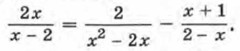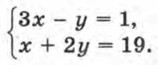Уравнения (продолжение)

20. Теорема Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Иначе говоря, если х₁ и х₂ — корни уравнения х² + рх + q = 0, то x₁ + x₂ = -p и x₁x₂ = g.

Из теоремы Виета следует, что если х₁ и х₂ — корни квадратного уравнения ах² + bх + с = 0, то

Теорема, обратная теореме Виета: если числа m и n таковы, что их сумма равна -р, а произведение равно q, то эти числа являются корнями уравнения х² + рх + q — 0.

21. При решении дробных рациональных уравнений целесообразно поступать следующим образом:

1) найти общий знаменатель дробей, входящих в уравнение;
2) умножить обе части уравнения на общий знаменатель;
3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.

Решим, например, уравнение

Умножив обе части уравнения на общий знаменатель дробей, т. е. на х(х - 2), получим 2х² = 2 + х(х + 1). Это уравнение приводится к квадратному уравнению х² - х - 2 = 0, имеющему корни 2 и -1. При х = 2 общий знаменатель дробей исходного уравнения обращается в нуль, этот корень нужно исключить. При х = - 1 общий знаменатель х(х - 2) в нуль не обращается, следовательно, число -1 является корнем исходного уравнения.

22. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Например, пара чисел х = -5, у = 3 является решением уравнения х² - 4у = 13. Это решение можно записать так: (-5; 3).

Линейным уравнением с двумя переменными называется уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.

23. Каждое решение (х; у) уравнения с двумя переменными можно изобразить в координатной плоскости точкой с координатами х и у. Все такие точки образуют график уравнения.

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

24. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Например, пара чисел х = 3, у = 8 — решение системы

Решить систему уравнений — значит найти все ее решения или доказать, что решений нет.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы уравнений, не имеющие решений, также считают равносильными.

Для решения систем уравнений с двумя переменными используются способ подстановки, способ сложения, графический способ.

<<< К началу