|
|
|
|
|
§ 3. Квадратичная функция и ее график Функция у = ах2, ее график и свойства (продолжение)Построим график функции
Воспользовавшись этой таблицей, построим график функции
Сравним графики функций Вообще графики функций у = ах2 и у = -ах2 (при а ≠ 0) симметричны относительно оси х. График функции у = ах2, где а ≠ 0, как и график функции у = х2, называется параболой. Сформулируем свойства функции у = ах2 при а > 0.
Докажем свойство 4.
Так как а > 0 и х2 - х1 > 0, то произведение а(х2 - x1)(x2 + х1) имеет тот же знак, что и множитель х2 + х1. Если числа х2 и х1 принадлежат промежутку (-∞; 0], то этот множитель отрицателен. Если числа х2 и х1 принадлежат промежутку [0; +∞), то множитель х2 + x1 положителен. В первом случае у2 - у1 < 0, т. е. у2 < у1; во втором случае у2 - у1 > 0, т. е. у2 > у1. Значит, в промежутке (-∞; 0] функция убывает, а в промежутке [0; +∞) возрастает. Теперь сформулируем свойства функции у = ах2 при а < 0.
Доказательство свойства 4 проводится аналогично тому, как это было сделано для функции у = ах2 при а > 0. Из перечисленных свойств следует, что при а > 0 ветви параболы у = ах2 направлены вверх, а при а < 0 — вниз. Ось у является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы у = ах2 является начало координат. Построение графика, симметричного данному относительно оси х, растяжение графика от оси х или сжатие к оси х — различные виды преобразования графиков функции. Преобразования графиков, рассмотренные нами для функции у = ах2, применимы к любой функции. График функции у = -ƒ(x) можно получить из графика функции у = ƒ(x) с помощью симметрии относительно оси х. График функции у = aƒ(x) можно получить из графика функции у = ƒ(x) с помощью растяжения от оси х в а раз, если а > 1, и с помощью сжатия к оси х в
|
|
|



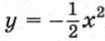 , для чего составим таблицу значений этой функции:
, для чего составим таблицу значений этой функции:

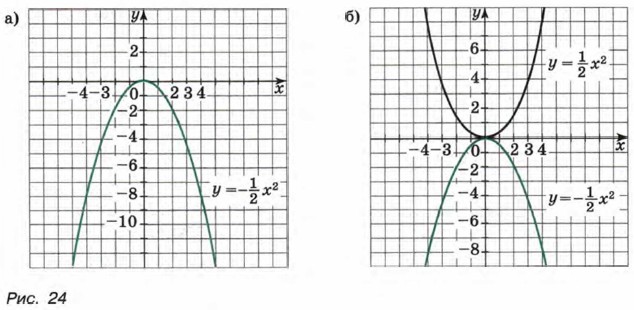
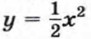 (рис. 24, б). При любом х значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. Иными словами, график функции
(рис. 24, б). При любом х значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. Иными словами, график функции  Пусть х1 и х2 — два значения аргумента, причем х2 > х1, а у1 и у2 — соответствующие им значения функции. Составим разность у2 - у1 и преобразуем ее:
Пусть х1 и х2 — два значения аргумента, причем х2 > х1, а у1 и у2 — соответствующие им значения функции. Составим разность у2 - у1 и преобразуем ее:
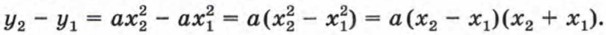

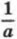 раза, если 0 < а < 1.
раза, если 0 < а < 1.