|
|
|
|
|
§ 3. Квадратичная функция и ее график Функция у = ах2, ее график и свойстваОдной из важных функций, к изучению которой мы переходим, является квадратичная функция.
Областью определения квадратичной функции является множество всех чисел. Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением а (м/с2) и к началу отсчета времени t прошло путь s0 (м), имея в этот момент скорость υ0 (м/с), то зависимость пройденного пути s (м) от времени t (с) выражается формулой
Если, например, а = 6, υ0 = 5, s0 = 20, то s = 3t2 + 5t + 20. Изучение квадратичной функции начнем с частного случая — функции у = ах2. При а = 1 формула у = ах2 принимает вид у = х2. С этой функцией вы уже встречались. Ее графиком является парабола. Построим график функции у = 2х2. Составим таблицу значений этой функции:
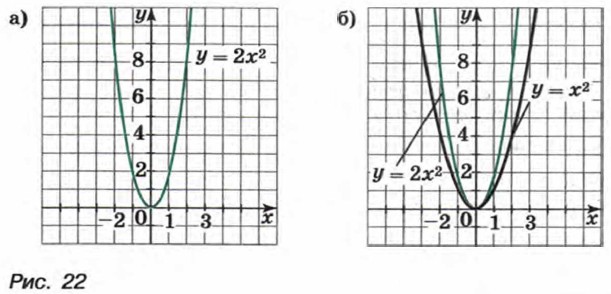
Построим точки, координаты которых указаны в таблице. Соединив их плавной линией, получим график функции у = 2х2 (рис. 22, а). При любом х ≠ 0 значение функции у = 2х2 больше соответствующего значения функции у = х2 в 2 раза. Если переместить каждую точку графика функции у = х2 вверх так, чтобы расстояние от этой точки до оси х увеличилось в 2 раза, то она перейдет в точку графика функции у = 2x2. При этом каждая точка графика функции у = 2х2 может быть получена из некоторой точки графика функции у = х2. Иными словами, график функции у = 2х2 можно получить из параболы у = х2 растяжением от оси х в 2 раза (рис. 22, б).
Построим теперь график функции
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции При любом х ≠ 0 значение функции
Вообще график функции у = ах2 можно получить из параболы у = х2 растяжением от оси х в а раз, если а > 1, и сжатием к оси х в Рассмотрим теперь функцию у = ах2 при а < 0.
|
|
|



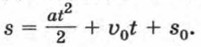

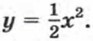 Для этого составим таблицу ее значений:
Для этого составим таблицу ее значений:

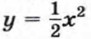 (рис. 23, а).
(рис. 23, а).
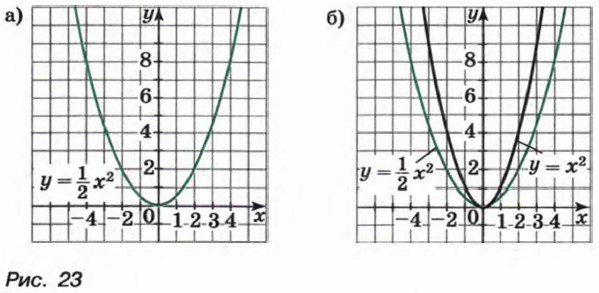
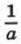 раза, если 0 < а < 1.
раза, если 0 < а < 1.