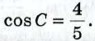|
|
|
|
|
§ 3. Скалярное произведение векторов Задачи к § 3. Скалярное произведение векторов (окончание)Применение скалярного произведения векторов к решению задач1054. Решение Точка М — середина отрезка ВС, поэтому
или 4AM2 = АВ2 + АС2 + 2 АВ • АС • cos А. Второе утверждение задачи докажите самостоятельно. 1055. Найдите угол, лежащий против основания равнобедренного треугольника, если медианы, проведённые к боковым сторонам, взаимно перпендикулярны. Решение Пусть АВС — равнобедренный треугольник с основанием АВ и AA1, ВВ1 — его медианы, проведённые к боковым сторонам (рис. 305). Введём обозначения
По условию задачи АA1 ⊥ BB1 и, следовательно, 1056. Докажите, что диагонали ромба взаимно перпендикулярны. Ответы к задачам § 3. Скалярное произведение векторов1039. а) 45°; б) 90°; в) 90°; г) 90°; д) 180°; е) 90°; ж) 135°; з) 0°. 1040. а) 60°; б) 120°; в) 120°; г) 90°; д) 0°; е) 180°. 1041. а) 3√2; б) 0; в) -3√2. 1042. 1043. 13. 1044. а) -2,5; б) 0; в) 5. 1047. а) x =7,5; 1048. 1049. ∠A ≈ 60°, ∠B ≈ 21°47', ∠C ≈ 98°13'. 1050. √129 и 7. 1051. 3. 1052. 13. 1053. -5.
|
|
|



 Докажите, что если AM — медиана треугольника АВС, то 4АМ2 = АВ2 + АС2 + 2АВ • АС • cos А. Пользуясь этой формулой, докажите, что медианы равнобедренного треугольника, проведённые к боковым сторонам, равны.
Докажите, что если AM — медиана треугольника АВС, то 4АМ2 = АВ2 + АС2 + 2АВ • АС • cos А. Пользуясь этой формулой, докажите, что медианы равнобедренного треугольника, проведённые к боковым сторонам, равны.
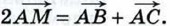 Отсюда получаем
Отсюда получаем
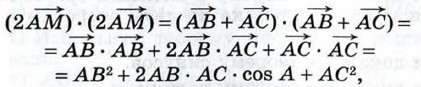
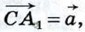
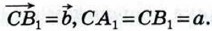 Тогда
Тогда 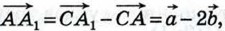
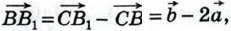 поэтому
поэтому
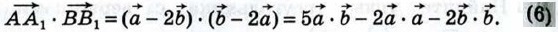
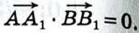 Далее,
Далее,  •
•  = a2 cos С,
= a2 cos С, 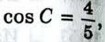 ∠C ≈ 36°52'.
∠C ≈ 36°52'.
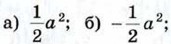 в) 0; г) а2.
в) 0; г) а2.
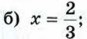 в) х = 0.
в) х = 0.
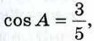 cos В = 0,
cos В = 0,