|
§ 3. Скалярное произведение векторов



Задачи к § 3. Скалярное произведение векторов
1039.  Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: 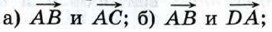 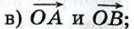 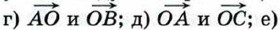 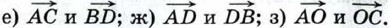
1040.  Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба. Найдите угол между векторами: Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба. Найдите угол между векторами: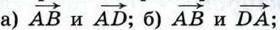 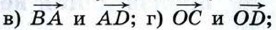 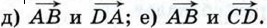
1041.  Вычислите скалярное произведение векторов Вычислите скалярное произведение векторов  и и  , если | , если | | = 2, | | = 2, | | = 3, а угол между ними равен: а) 45°; б) 90°; в) 135°. | = 3, а угол между ними равен: а) 45°; б) 90°; в) 135°.
1042.  В равностороннем треугольнике АВС со стороной а проведена высота BD. Вычислите скалярное произведение векторов: В равностороннем треугольнике АВС со стороной а проведена высота BD. Вычислите скалярное произведение векторов:
1043.  К одной и той же точке приложены две силы К одной и той же точке приложены две силы 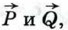 действующие под углом 120° друг к другу, причём действующие под углом 120° друг к другу, причём 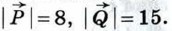 Найдите величину равнодействующей силы Найдите величину равнодействующей силы 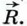
1044.  Вычислите скалярное произведение векторов Вычислите скалярное произведение векторов  и и  , если: , если:
1045. Докажите, что ненулевые векторы  {х; у} и {х; у} и  {-у; х} перпендикулярны. {-у; х} перпендикулярны.
1046. Докажите, что векторы 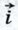 + + 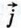 и и 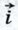 - - 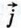 перпендикулярны, если перпендикулярны, если 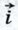 и и 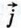 — координатные векторы. — координатные векторы.
1047.  При каком значении х векторы При каком значении х векторы  и и  перпендикулярны, а) перпендикулярны, а)  {4; 5}, {4; 5},  {x; -6}; б) {x; -6}; б)  {x; -1}, {x; -1},  {3; 2}; в) {3; 2}; в)  {0; -3}, {0; -3},  {5; x}? {5; x}?
1048.  Найдите косинусы углов треугольника с вершинами А (2; 8), В (-1; 5), С (3; 1). Найдите косинусы углов треугольника с вершинами А (2; 8), В (-1; 5), С (3; 1).
1049.  Найдите углы треугольника с вершинами А (-1; √3), В (1; -√3) и Найдите углы треугольника с вершинами А (-1; √3), В (1; -√3) и 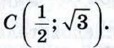
1050.  Вычислите | Вычислите | + +  | и | | и | - -  |, если | |, если | | = 5, | | = 5, | , , 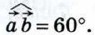
1051.  Известно, что Известно, что 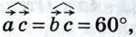 | | |=1, |=1, 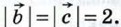 Вычислите Вычислите 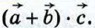
1052.  Вычислите скалярное произведение векторов Вычислите скалярное произведение векторов 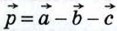 и и 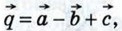 если | если | | = 5, | | = 5, | | = 2, | = 2, 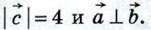
1053.  Вычислите скалярное произведение векторов Вычислите скалярное произведение векторов  и и  и и 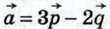 где где 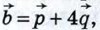 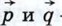 — единичные взаимно перпендикулярные векторы. — единичные взаимно перпендикулярные векторы.
Окончание >>>
|