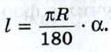Длина окружности

Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана из тонкой нерастяжимой нити. Если мы разрежем нить в какой-нибудь точке А и распрямим её, то получим отрезок АА₁ ( длина которого и есть длина окружности (рис. 312).

Рис. 312

Периметр любого правильного вписанного в окружность многоугольника является приближённым значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее это приближённое значение, так как многоугольник при увеличении числа сторон всё ближе и ближе «прилегает» к окружности (рис. 313). Точное значение длины окружности — это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.

Рис. 313

Выведем формулу, выражающую длину окружности через её радиус. Пусть С и С' — длины окружностей радиусов R и R'. Впишем в каждую из них правильный n-угольник и обозначим через Р_n и R'_n их периметры, а через а_n и а'_n — их стороны. Используя формулу (2) из § 1, получаем:

Следовательно,

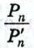Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как Р_n → С, Р'_n → С' при n → ∞, то предел отношения равен 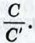С другой стороны, в силу равенства (1) этот предел равен 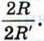Таким образом, 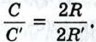Из этого равенства следует, что 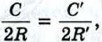т. е. отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π (читается «пи»).

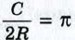Из равенства получаем формулу для вычисления длины окружности радиуса R:

С = 2πR.

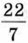Доказано, что π является бесконечной непериодической десятичной дробью, т. е. иррациональным числом. Рациональное число является приближённым значением числа л с точностью до 0,002. Это приближённое значение было найдено ещё в III в. до н. э. великим греческим учёным Архимедом. При решении задач обычно пользуются приближённым значением π с точностью до 0,01: π = 3,14.

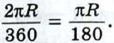Выведем теперь формулу для вычисления длины l дуги окружности с градусной мерой α. Так как длина всей окружности равна 2πR, то длина дуги в 1° равна Поэтому длина l выражается формулой