|
§ 10. Представление чисел в позиционных системах счисления



Перевод чисел из q-ичной в десятичную систему счисления
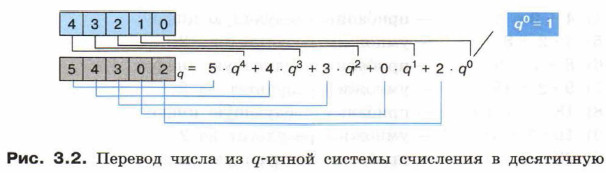
Перевод числа, записанного в системе счисления с основанием q, в десятичную систему счисления основан на использовании развёрнутой формы записи чисел (рис. 3.2).
|
 Для перевода числа Aq в десятичную систему счисления достаточно: Для перевода числа Aq в десятичную систему счисления достаточно:
1) записать развёрнутую форму числа Aq:
2) представить все числа, фигурирующие в развёрнутой форме, в десятичной системе счисления;
3) вычислить значение полученного выражения по правилам десятичной арифметики.
|
Переведём числа 2123, 1235 и 12А16 в десятичную систему счисления:
2123 = 2 • 32 + 1 • 31 + 2 • 30 = 2 • 9 + 1 • 3 + 2 • 1 = 2310;
1235 = 1 • 52 + 2 • 51 + 3 • 50 = 2 • 25 + 2 • 5 + 3 • 1 = 6310;
12А16 = 1 • 162 + 2 • 161 + А • 160 = 1 • 256 + 2 • 16 + 10 • 1 = 29810.
Перевод в десятичную систему счисления целых двоичных чисел будет значительно проще, если вспомнить и использовать уже знакомую вам таблицу степеней двойки:
Например:
Для перевода двоичного числа в десятичную систему счисления можно воспользоваться схемой Горнера:
1) 1 • 2 = 2 — возьмем 1, соответствующую самому старшему разряду числа, и умножим её на 2;
2) 2 + 0 = 2 — прибавим следующую цифру;
3) 2 • 2 = 4 — умножим результат на 2;
4) 4 + 0 = 4 — прибавим следующую цифру;
5) 4 • 2 = 8 — умножим результат на 2;
6) 8 + 1 = 9 — прибавим следующую цифру;
7) 9 • 2 = 18 — умножим результат на 2;
8) 18 + 1 = 19 — прибавим следующую цифру;
9) 19 • 2 = 38 — умножим результат на 2;
10) 38 + 1 = 39 — прибавим следующую цифру;
11) 39 • 2 = 78 — умножим результат на 2;
12) 78 + 0 = 78 — прибавим следующую цифру;
13) 78 • 2 = 156 — умножим результат на 2;
14) 156 + 0 = 156 — прибавим следующую цифру;
15) 156 • 2 = 312 — умножим результат на 2;
16) 312 + 1 = 313 — прибавим следующую цифру;
17) 313 • 2 = 626 — умножим результат на 2;
18) 626 + 1 = 627 — прибавим последнюю цифру.
Рассмотрим несколько примеров решения задач.
  Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления. Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.
Запишем условие задачи иначе: 212q = 5710, q > 2.
Представим в виде суммы разрядных слагаемых:
Решим уравнение:
2q2 + q + 2 = 57.
2q2 + q - 55 = 0.
Это квадратное уравнение, его корни хх = -5,5; х2 = 5.
Так как основание системы счисления должно быть натуральным числом, то q = 5.
Окончание >>>
| 


 Для перевода числа Aq в десятичную систему счисления достаточно:
Для перевода числа Aq в десятичную систему счисления достаточно:

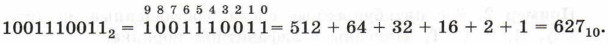

 Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.
Пример 1. Десятичное число 57 в некоторой системе счисления записывается как 212. Определим основание этой системы счисления.