|
|
|
|
|
§ 10. Представление чисел в позиционных системах счисления 10.3.Перевод чисел из q-ичной в десятичную систему счисления
Все пятибуквенные слова, составленные из пяти букв А, И, Р, С, Т, записаны в алфавитном порядке. Вот начало списка: 1. ААААА
Необходимо найти ответы на два вопроса. 1. На каком месте от начала списка стоит слово ИСТРА? 2. Сколько всего слов в этом списке? Введём следующие обозначения: А — 0, И — 1, Р — 2, С — Т — 4. Перепишем в новых обозначениях исходный список: 1. 00000
Теперь перед нами последовательность чисел от 0 до 44444, записанных в пятеричной системе счисления. При этом на 1-м месте в этой последовательности находится 0, на 2-м месте — 1, на 3-м месте — 2 и т. д. Это значит, что само число на единицу меньше того места (номера), которое оно занимает в последовательности. Представив слово ИСТРА в новых обозначениях, получим 134205. Переведём это пятеричное число в десятичную систему счисления: 134205 = 1 • 54 + 3 • 53 + 4 • 52 + 2 • 51 + 0 • 50 =
Это число находится в списке на 1111-м месте. Чтобы выяснить, сколько всего слов в списке, запишем его самое последнее слово: ТТТТТ. Ему соответствует число 444445. 444445 = 4 • 54 + 4 • 53 + 4 • 52 + 4 • 51 + 4 • 50 = 312410. В списке это число стоит на 3125-м месте.
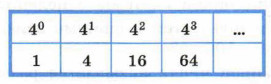
В четверичной системе счисления используются цифры 0, 1, 2 и 3; число представляется в виде суммы разрядных слагаемых:
Из этой таблицы видно, что интересующие нас числа (≤ 60) не будут более чем трёхзначными. С учётом того что их запись заканчивается на 31, определим первую цифру (k): k • 16 + 3 • 4 + 1 ≤ 60, k • 16 ≤ 47, k ∈ {0, 1, 2}. Искомые числа: 314 = 1310 (k = 0), 1314 = 2910 (k = 1), 2314 = 4510 (k = 2).
|
|
|




 Пример 2.
Пример 2.
 Вспомните о комбинаторике и предложите другой способ подсчёта количества слов в нашем списке.
Вспомните о комбинаторике и предложите другой способ подсчёта количества слов в нашем списке.