|
|
|
|
|
§ 1. Делимость чисел 2. Признаки делимости на 10, на 5 и на 2 (окончание)45. Подтвердите примерами следующее свойство суммы: а) если каждое слагаемое кратно числу а, то и сумма кратна числу а; б) если только одно слагаемое суммы не кратно числу а, то сумма не кратна числу а. 46. Назовите наименьший и наибольший делители числа 24. Назовите наименьшее кратное числу 24. Есть ли у этого числа наибольшее кратное? Назовите какое-нибудь число, кратное и 5, и 12. 47. Запишите все двузначные числа, являющиеся: а) делителями 100;
48. Число b является делителем числа а. Докажите, что частное от деления а на b также является делителем числа а. Проверьте это утверждение, если а = 18, а b = 3. 49. Докажите, что: а) если а кратно b, а b кратно с, то а кратно с;
50. Какие из дробей 51. При каких натуральных значениях а дробь 52. Решите уравнение: а) (х + 2,3) • 0,2 = 0,7; в) 4,2х + 8,4 = 14,7;
53. На уроке физкультуры Андрей, Марат, Костя, Саша, Петя и Серёжа готовятся к прыжкам в высоту. а) Сколькими способами можно установить для них очерёдность прыжков? б) Сколькими способами можно установить очерёдность прыжков, если начинают обязательно Костя или Саша? 54. Решите задачу: 1) Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал? 2) Я задумал число. Если его увеличить на 9,2 и результат увеличить в 11 раз, то получится 110. Какое число я задумал? 55. Найдите среди чисел 154, 161, 174, 178, 191, 315, 320, 346, 425, 475 числа: а) кратные 2; б) кратные 5; в) кратные 10; г) нечётные. 56. Напишите: а) все чётные числа, большие 10 и меньшие 21;
57. Напишите три четырёхзначных числа, кратных 5. 58. Выберите из дробей 59. Решите уравнение: а) (4,9 - х) : 1,2 = 3; б) 3,8 • (х - 0,2) = 2,28. 60. Найдите значение выражения: а) (93 • 7 + 141) : 72;
|
|
|



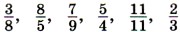 являются правильными и какие — неправильными?
являются правильными и какие — неправильными?
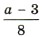 будет правильной и при каких натуральных значениях b дробь
будет правильной и при каких натуральных значениях b дробь 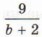 будет неправильной?
будет неправильной?
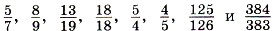 сначала все правильные дроби, а затем неправильные.
сначала все правильные дроби, а затем неправильные.