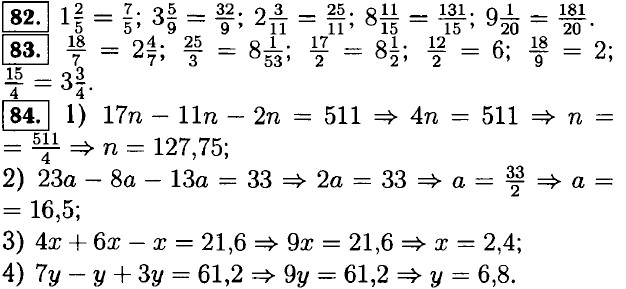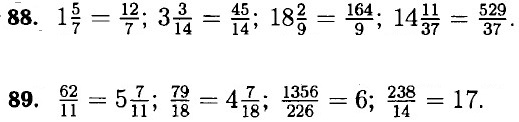Признаки делимости на 9 и на 3. Домашние работы

61. Сумма чисел — 7 + 5 + 4 + 3 + 2 = 21 делится на 3, следовательно и число 75432 делится на 3; 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33 делится на 3, и число 2 772 825 делится на 3; 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18 делится на 3 и на 9, а следовательно число 5402 070 делится на 3 и на 9.

62. 1116, 2223, 8001.

63. 2*5 - 225, 255, 285;
46* - 462, 465, 468;
*14 - 114, 414, 714.

64. а) 111, 111111, 111111111;
б) 666, 666666, 666666666.

65. Нет. Например 13, 23 не делятся на 3.

66. В подарках может быть только 75 (7 + 5 = 12) или 63 (6 + 3 = 9) конфеты, так как эти числа делятся на 3.

67. В коровнике может быть только 288 (2 + 8 + 8 = 18) коров, так как это число делится на 9.

68. 200 - 60 = 140, 1 + 4 + 0 = 5; 60 кг остаться не может.
200 - 56 = 144, 1 + 4 + 4 = 9; 56 кг может остаться.

69. а) 6,14; 7,85; 3,467; 20,2; 3,4;
б) 0,55; 3,5; 0,58; 1,7; 4,92;
в) 1,5; 2; 1; 29; 0,31;
г) 0,05; 2,6; 0,2; 20; 20.

70. а) 18 • 5 = 90, 90 : 2 = 45, 90 : 10 = 9;
б) 1 • 10 = 10, 10 • 5 = 50, 50 • 3 = 150, 150 • 2 = 300.

71. а) чётным; б) нечётным; в) чётным

72. а) верно (20 кратно 2); б) верно (20 кратно 5); в) верно (20 кратно 4); г) зависит от значения ширины.

73. а) 15,3 • 0,05 +1,4 = 0,765 +1,4 = 2,165; б) (8,6 + 2,2) • 0,3 = 10,8 • 0,3 = 3,24.

74. а) Неверно, например: 4 + 5 = 9 кратно 3;
б) пусть даны два кратных а числа: х₁ = n • а и х₂ = m • а, где n и m — натуральные числа. х₁ - х₂ = n • а - m • а = (n - m) • а. Тое сть разница таких чисел всегда кратна а.

75. Надо определить последнюю цифру суммы:
а) 37843 + 54321 =.....4, делится на 2; 48345 + 75 634 = .....9, не делится на 2; 37244 + 52 486 = .....0, делится на 2;
б) 87338 - 56893 =......5, не делится на 2; 153847 - 112 353 = .....4, делится на 2; 84 537 - 26237 = .....0, делится на 2.

76. Нет, числа оканчивающиеся на 5 не делятся на 10.

77. Числа, оканчивающиеся на 0, делятся на 5.
Число, оканчивающееся 5, всегда делятся на 5

78. а) цифрой 0; б) цифрой 5

79. а) 0 или 5; б) любая цифра; в) при любой цифре число не будет делиться на 5.

80. Нечётные цифры; 1, 3, 5, 7, 9. В разряд единиц, десяток и сотен — одна цифра из пяти, следовательно число таких чисел 5 • 5 • 5 = 125.

81. Если стоит 0, то первые две цифры от 10 до 99 (99 - 10 + 1 = 90 штук), за исключением сдвоенных 11, 22, ... 99 (9 штук) и с нулем 10, 20, ... 90 (9 штук). Значит всего таких чисел 90 - 9 - 9 = 72. Если стоит 0, то первые две цифры от 10 до 99 (99 - 10 + 1 = 90 штук), за исключением сдвоенных 11, 22, ... 99 (9 штук), с пятеркой 15, 25, ... 50, 51, ... 95 (17 штук) (без 55) (17 штук). Значит всего таких чисел 90 - 9 - 17 = 64.
Всего получается 72 + 64 = 136 чисел.

85. 0,5632 : 5,12 + 42,56 : 3,8 - (11-3,9 : 1,5) = 0,11 + 11,2 - (11 - 2,6) = 11,31 - 8,4 = 2,91.

86. Кратны 3 числа: 240, 246, 252.
На 9 делится 252.

87. 6723; 5436; 1116.

90. Упростим выражение: 4,7k + 5,3k - 0,83 = 10k - 0,83; если k = 0,83, то 10k - 0,83 = 10 • 0,83 - 0,83 = 8,3 - 0,83 = 7,47; если k = 8,3, то 10k - 0,83 = 10 • 8,3 - 0,83 = 83 - 0,83 = 82,17; если k = 0,083, то 10k - 0,83 = 10 • 0,083 - 0,83 = 0,83 - 0,83 = 0.

91. а) х + 3х + 5 = 17 ⇒ 4х + 5 = 17 ⇒ 4х = 12 ⇒ х = 3;
б) 3,5х + 2,2х - 4,56 ⇒ 5,7х = 4,56 ⇒ х = 0,8;
в) 3,2у - 2,7у = 0,6 ⇒ 0,5у = 0,6 ⇒ у = 1,2;
г) 3,7z - z = 0,54 ⇒ 2,7z = 0,54 ⇒ z = 0,2.

92. (5,98 + 5,36) : 2,8 : (5 • 0,003 + 15 • 0,029) = 11,34 : 2,8 : (0,015 + 0,435) = 11,34 : 2,8 : 0,45 = 4,05 : 0,45 = 9.

<<< К началу