Главная >> Математика 6 класс с ГДЗ. Виленкин

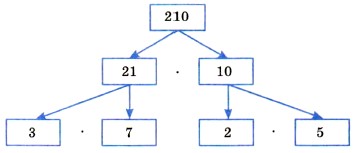
§ 1. Делимость чисел

5. Разложение на простые множители

Число 210 является произведением чисел 21 и 10. Значит, 210 = 21 • 10. Числа 21 и 10 составные. Их тоже можно представить в виде произведений: 21 = 3 • 7 , 10 = 2 • 5. Получаем: 210 = 3 • 7 • 2 • 5. Теперь в произведении 3 • 7 • 2 • 5 все множители — простые числа. Таким образом, число 210 разложено на простые множители:

Число 210 можно разложить на простые множители иным способом: 210 = 30 • 7 = 10 • 3 • 7 = 5 • 2 • 3 • 7 . Получились те же самые простые множители, только записанные в другом порядке. Обычно записывают множители в порядке их возрастания:

210 = 2 • 3 • 5 • 7.

Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.

При разложении чисел на простые множители используют признаки делимости.

Разложим, например, на простые множители число 756. Оно делится на 2, так как оканчивается чётной цифрой 6. Имеем 756 : 2 = 378. Проведём вертикальную черту и запишем слева от неё делимое 756, а справа — делитель 2. Частное запишем под числом 756.

Число 378 тоже делится на 2. При делении получаем в частном 189.

189 не делится на 2, так как оканчивается нечётной цифрой. Но 189 делится на 3, так как сумма его цифр (1 + 8 + 9 = 18) делится на 3. Имеем 189 : 3 = 63.
Число 63 также делится на 3. При делении получим число 21.
Число 21 также делим на 3, причём получаем в частном простое число 7.
При делении числа 7 на 7 получаем 1.
Разложение на множители закончено.
Значит, 756 = 2 • 2 • 3 • 3 • 3 •7.

Существуют ли составные числа, которые нельзя разложить на простые множители?
Чем могут отличаться два разложения одного и того же числа на простые множители?

121. Разложите на простые множители числа:

а) 216; 162; 144; 512; 675; 1024;
б) 60; 180; 220; 350; 400; 1200; 8000;
в) 11; 1001; 1225; 21780; 45 630.

122. Напишите все двузначные числа, разложение которых на простые множители состоит:

а) из двух одинаковых множителей;
б) из трёх одинаковых множителей.

123. Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен:

а) 11;
6)13;
в) 23;;
г) 47.

124. Выясните, делится ли число а на число b без остатка, если:

а) а = 2 • 2 • 2 • 3 • 5 • 7 и b = 2 • 3 • 7;
б) а = 3 • 3 • 5 • 5 • 11 и b = 3 • 3 • 5 ;
в) а = 3 • 3 • 5 • 7 • 13 и b = 3 • 5 • 5 • 1 3 ;
г) а = 2 • 3 • 3 • 7 • 7 и b = 21;
д) а = 2 • 2 • 3 • 3 • 3 • 5 • 7 и b = 135;
е ) а = 2 • 2 • 2 • 3 • 3 • 5 • 5 и b = 1000.

В случае, когда а делится на b, найдите частное.

125. Вычислите устно:

126. При каких натуральных значениях а произведение 23а является простым числом?

127. Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр — простым числом?

128. Найдите по два простых делителя каждого из чисел:

54;62;143;182; 3333; 5005.

129. Какие простые числа являются решениями неравенства 17 < р < 44?

Окончание >>>