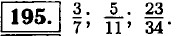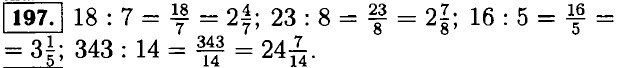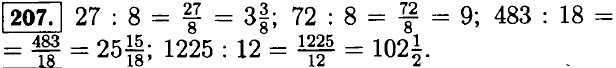Наименьшее общее кратное. ГДЗ к учебнику

194. На место сотен место можно поставить одну из 4-х цифр (2, 4, б, 8). На место десятков и единиц 3-е место можно поставить одну из 5-и цифр (0, 2, 4, б, 8). В итоге можно получить: 4 • 5 • 5 = 100.

196. 6 : 11; 19 : 9; 37 : 10; 6 : 10; 13 : 100.

198. (3,8 + 4,2 + 3,5 + 4,1) : 4 = 15,6 : 4 = 3,9.

199. Пусть х — первое число, тогда второе число — 2х. Составим и решим уравнение: (х + 2х) : 2 = 54 ⇒ 3x : 2 = 54 ⇒ 3х = 108 ⇒ х = 36, 2х = 72.

200. 1) Составим и решим уравнение: 2,4x + х = 9,1 = 38 ⇒ 3,4x = 28,9 ⇒ х = 8,5 ⇒ 2,4x = 2,4 ⇒ 8,5 = 20,4 т керосина было израсходовано.
2) Составим и решим уравнение: х + 3,2x + 4,3 = 19 ⇒ 4,2x = 19 4,3 ⇒ 4,2x = 14,7 ⇒ х = 3,5 ⇒ 3,2x = 11,2 т муки было выдано до обеда.

201. 1-я сотня — 25, 2-я сотня — 21, 3-я сотня — 16 и далее: 16, 17, 14. 16, 14, 15, 14. Какой-либо закономерности в расположении простых чисел не наблюдается. В таблице всего 35 пар чисел-близнецов: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883). Самая большая пара чисел-близнецов 881 и 883. Среди первых 500 натуральных чисел 24 пары чисел-близнецов, среди чисел от 500 до 1000 — 11 пар.

202. а) НОК(18; 45) = НОК(2 • 3 • 3; 3 • 3 • 5) = 2 • 3 • 3 • 5 = 90; б) НОК(30; 40) = НОК(30 = 2 • 3 • 5; 2 • 2 • 2 • 5) = 2 • 2 • 2 • 3 • 5 = 120; в) НОК(210; 350) = НОК(2 • 3 • 5 • 7; 2 • 5 • 5 • 7) = 2 • 3 • 5 • 5 • 7 = 1050; г) НОК(20; 70; 15) = НОК(2 • 2 • 5; = 2 • 5 • 7; 3 • 5) = 2 • 2 • 3 • 5 • 7 = 420.

203. а) НОК(а, b) = 5 • 5 • 7 • 7 • 13 = 15 925;
б) НОК(а, b) = НОК(504,540) = НОК(2 • 2 • 2 • 3 • 3 • 7,2 • 2 • 3 • 3 • 3 • 5) = 2 • 2 • 2 • 3 • 3 • 3 • 5 • 7 = 7560.

204. Пусть Саша собрал х стаканов малины, тогда Серёжа 2х стаканов, а Коля х + 3. Все вместе мальчики собрали 51 стакан. Составим и решим уравнение: х + 2х + 3 + х = 51 ⇒ 4х = 48 ⇒ х = 12 стаканов собрала Саша. Серёжа собрал: 2х = 24 стакана. Коля собрал: х + 3 = 15 стаканов.

205. Пусть х кг масса первого спутника. Тогда масса второго спутника х + 424,7 кг, а масса третьего х + 424,7 + 818,7 кг. Масса всех трёх спутников — 1918,9 кг. Составим И решим уравнение: х + х + 424,7 + х + 424,7 + 818,7 = 1918,9 ⇒ 3х = 250,8 ⇒ х = 83,6 кг — масса первого спутника. Масса второго спутника: х + 424,7 = 508,3 кг. Масса третьего спутника: х + 424,7 + 818,7 = 1327 кг.

206. а) (х + 36,1) • 5,1 = 245,82; х + 36,1 = 48,2; х = 12,1; б) (m - 0,67) • 0,02 = 0,0152; m - 0,67 = 0,76; m = 1,43; в) (х + 24,3) : 18,3 = 3,1; х + 24,3 = 3,1 • 18,3; х + 24,3 = 56,73; х = 32,43; г) (у -15,7) : 19,2 = 4,7; у - 15,7 = 4,7 • 19,2; у - 15,7 = 105,94.

208. (5,24 + 6,97 + 8,56 + 7,32 + 6,23) : 5 = 34,32 : 5 = 6,864.

209. Всего поезд проехал: 65,2 • 3 + 83,3 • 2 = 195,6 + 166,6 = 362,2 км. Средняя скорость за 5 часов пути равна: 362,3 : 5 = 72,44 км/ч.

210. а) 51 - (3,75 : 3 + 86,45 : 24,7) • 2,4 = 51-(1,25 = 3,5) • 2,4 = 51 - (1,25 - 3,5) • 2,4 = 51 -11,4 = 39,64;
б) (650 000 : 3125 -196,5) • 3,14 = (208 - 196,5) • 3,14 = 36,11.

<<< К началу