|
|
|
|
|
§ 59. Закон Ома для полной цепи Закон Ома для полной цепи (окончание)Максимальное напряжение на полюсах источника равно Следовательно, напряжение между разомкнутыми полюсами источника тока равно ЭДС этого источника. Минимальное же напряжение между полюсами источника равно нулю. Это имеет место при коротком замыкании, когда внешнее сопротивление R = 0. В этом случае сила тока максимальна. Её называют силой тока короткого замыкания.
Подсказка. Воспользуйтесь законом Ома для полной цепи. Из формулы (9) видно, что при очень малом внутреннем сопротивлении источника (как, например, у автомобильного аккумулятора) сила тока короткого замыкания будет очень большой, что может вывести источник тока из строя.
а) Как изменилось полное сопротивление цепи? б) Чему равно внутреннее сопротивление батарейки? Измерив напряжение на полюсах источника и силу тока в цепи при двух различных значениях сопротивления внешней цепи, можно найти ЭДС
а) Постройте систему координат I, U и нанесите две точки графика зависимости U(I) согласно приведённым данным. б) Проведите прямую через эти точки и отметьте точки пересечения этой прямой с осями координат. Используя этот график, найдите, чему равны ЭДС, сила тока короткого замыкания и внутреннее сопротивление источника тока. в) Используя уравнение (8), составьте систему двух уравнений с двумя неизвестными
|
|
|



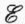 . Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
. Это имеет место при I = 0. Сила тока равна нулю, когда полюса источника разомкнуты (в этом случае внешнее сопротивление цепи является бесконечно большим).
 5. Покажите, что сила тока короткого замыкания выражается формулой
5. Покажите, что сила тока короткого замыкания выражается формулой
