|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа Основное уравнение молекулярно-кинетической теорииИмпульс средней силы, действующий на стенку со стороны всех молекулМолекулы со скоростями, близкими к υix, за время Δt меняют импульс стенки на
Согласно второму закону Ньютона импульс силы FΔt, действующей на стенку, равен изменению импульса стенки:
Выразим этот импульс силы через средний квадрат проекции скорости на ось X, который согласно формуле (4.3.3) определяется так:
где суммирование осуществляется по всем проекциям скоростей, как положительным, так и отрицательным. Но положительные значения проекций скоростей встречаются столь же часто, как и отрицательные. Поэтому
или, учитывая определение среднего квадрата (4.4.6), будем иметь
Заменяя в уравнении (4.4.5) сумму по проекциям скоростей ее выражением (4.4.7), получим средний импульс силы
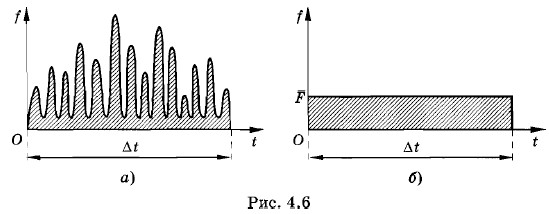
Этот результат можно пояснить графически. На рисунке 4.6, а изображена зависимость от времени силы ƒ, действующей на стенку при столкновении с нею различных молекул. Время соударения
Давление газаРазделив левую и правую части уравнения (4.4.8) на SAt и учитывая соотношение (4.3.6), найдем давление газа
Это и есть основное уравнение молекулярно-кинетической теории идеального газа*. * Это уравнение — первое количественное соотношение, полученное в молекулярно-кинетической теории. Поэтому его принято называть основным. Давление идеального газа пропорционально произведению массы молекулы на концентрацию молекул и средний квадрат их скорости. Формула (4.4.9) связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы, и является как бы мостом между двумя мирами: макроскопическим и микроскопическим. Если через
Отметим в заключение, что хотя расчет произведен без явного учета столкновений молекул, это не означает, что столкновения совсем не учитывались нами. Именно огромное число столкновений приводит к тому, что движение молекул является хаотическим. Равенства (4.3.4) и (4.3.6) выполняются с большой точностью как раз вследствие громадного числа столкновений.
|
|
|



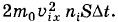 Изменение импульса стенки за время Δt всеми молекулами, столкнувшимися со стенкой, равно сумме выражений (4.4.3) по скоростям υix > 0 всех молекул:
Изменение импульса стенки за время Δt всеми молекулами, столкнувшимися со стенкой, равно сумме выражений (4.4.3) по скоростям υix > 0 всех молекул:
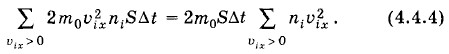
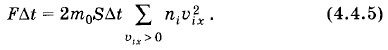

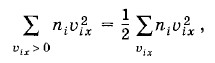
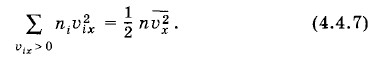

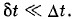 Сила меняется хаотически в зависимости от времени. Площадь под каждым пиком представляет собой импульс силы, действующей на стенку со стороны одной молекулы при соударении. Суммарная площадь под всеми пиками (ее численное значение) дает импульс силы, действующей на стенку за время Δt. Средний импульс силы
Сила меняется хаотически в зависимости от времени. Площадь под каждым пиком представляет собой импульс силы, действующей на стенку со стороны одной молекулы при соударении. Суммарная площадь под всеми пиками (ее численное значение) дает импульс силы, действующей на стенку за время Δt. Средний импульс силы 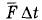 графически характеризуется площадью прямоугольника (рис. 4.6, б), равной суммарной площади импульсов сил от отдельных молекул.
графически характеризуется площадью прямоугольника (рис. 4.6, б), равной суммарной площади импульсов сил от отдельных молекул.

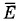 обозначить среднюю кинетическую энергию поступательного движения молекулы:
обозначить среднюю кинетическую энергию поступательного движения молекулы: 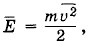 то уравнение (4.4.9) можно записать в форме
то уравнение (4.4.9) можно записать в форме
