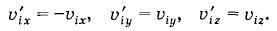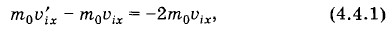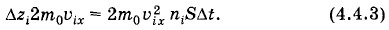|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа § 4.4. Основное уравнение молекулярно-кинетической теории
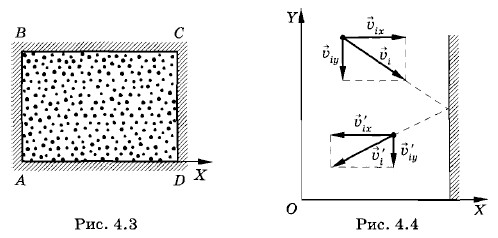
Пусть газ находится в прямоугольном сосуде с твердыми стенками. Газ и сосуд имеют одинаковые температуры, т. е. находятся в состоянии теплового равновесия. Будем считать столкновения молекул со стенками абсолютно упругими. При этом условии кинетическая энергия молекул в результате столкновения не меняется. Требование того, чтобы столкновения были абсолютно упругими, не является строго обязательным. В точности оно и не реализуется. Молекулы могут отражаться от стенки под разными углами и со скоростями, не равными по модулю скоростям до соударения. Но в среднем кинетическая энергия отраженных стенкой молекул будет равна кинетической энергии падающих молекул, если только существует тепловое равновесие. Результаты расчета не зависят от детальной картины столкновений молекул со стенкой. Поэтому вполне допустимо считать столкновения молекул подобными столкновениям упругих шаров с абсолютно гладкой твердой стенкой. Вычислим давление газа на стенку сосуда CD, имеющую площадь S и расположенную перпендикулярно оси X (рис. 4.3).
Пусть скорость
Объясняется это тем, что при абсолютно упругом ударе отсутствуют силы, параллельные стенке. Изменение проекций импульса молекулы на ось X равно
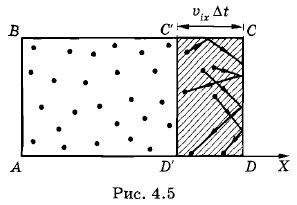
где m0 — масса молекулы. Согласно закону сохранения импульса стенке сосуда молекулой будет передан импульс 2m0υix. Следовательно, в соответствии со вторым законом Ньютона на стенку за время удара подействует импульс силы 2m0υix, направленный перпендикулярно стенке. Число соударений со стенкой молекул, скорости которых близки к υixЗа время Δt стенки могут достичь лишь молекулы со скоростями υix > 0, которые находятся от нее на расстоянии, не превышающем υixΔt (рис. 4.5). Эти молекулы движутся слева направо. Молекулы, находящиеся на больших расстояниях, не успеют долететь до стенки*. * Заметим, что столкновения молекул друг с другом не влияют на число их столкновений со стенкой. Если какая-либо молекула, у которой υix > 0, из-за столкновений не сможет достигнуть стенки, то ее место займет какая-то другая молекула. Давление определяется средним числом молекул с различными скоростями, которое не меняется в состоянии теплового равновесия при столкновениях. Не надо думать, что значения проекций скоростей υiy и υiz как-то влияют на достижение молекулами стенки CD. Если молекула столкнется со стенкой ВС или АВ (см. рис. 4.5), то проекция скорости υix при этом не изменится и молекула сместится вдоль оси X по-прежнему на отрезок υixΔt.
Выделенный объем CC'DD' равен υixΔtS. Число молекул в этом объеме со скоростями, близкими к υix, составляет Δzi = niυixΔtS, (4.4.2) где ni — число молекул со скоростями, близкими к υix > 0, в 1 см3. Импульс, переданный стенке молекулами со скоростями υix > 0Переданный молекулами (их число равно Δzi) импульс равен произведению Δzi на импульс, переданный одной молекулой (определяется по формуле (4.4.1)):
|
|
|



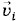 молекулы с номером i направлена под произвольным углом к стенке (рис. 4.4). При столкновении проекция скорости на ось X υix меняет знак, а проекции скорости на направления, совпадающие с осями Y и Z, υiy и υiz, остаются без изменения. После соударения
молекулы с номером i направлена под произвольным углом к стенке (рис. 4.4). При столкновении проекция скорости на ось X υix меняет знак, а проекции скорости на направления, совпадающие с осями Y и Z, υiy и υiz, остаются без изменения. После соударения