|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа
§ 4.5. Температура — мера средней кинетической энергии молекул
Для простоты будем считать количество газа равным 1 моль. Молярный объем газа обозначим через VM. Произведение молярного объема на концентрацию молекул представляет собой постоянную Авогадро NA, т. е. число молекул в 1 моль. Умножим обе части уравнения (4.4.10) на молярный объем VM и учтем, что nVM = NА. Тогда
Формула (4.5.1) устанавливает связь макроскопических параметров — давления р и объема VM — со средней кинетической энергией поступательного движения молекул. Вместе с тем полученное опытным путем уравнение состояния идеального газа для 1 моль имеет вид
Левые части уравнений (4.5.1) и (4.5.2) одинаковы, значит, должны быть равны и их правые части, т. е.
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекул и температурой:
Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Чем выше температура, тем быстрее движутся молекулы. Соотношение между температурой и средней кинетической энергией поступательного движения молекул (4.5.3) установлено для разреженных газов. Однако оно оказывается справедливым для любых веществ, движение атомов или молекул которых подчиняется законам механики Ньютона. Оно верно для жидкостей, а также для твердых тел, у которых атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решетки. При приближении температуры к абсолютному нулю энергия теплового движения молекул также приближается к нулю*. * При очень низких температурах (вблизи абсолютного нуля) движение атомов и молекул уже не подчиняется законам Ньютона. Согласно более точным законам движения микрочастиц — законам квантовой механики — абсолютный нуль соответствует минимальному значению энергии движения, а не полному прекращению какого- либо движения вообще. Постоянная БольцманаВ уравнение (4.5.3) входит отношение универсальной газовой постоянной R к постоянной Авогадро JVA. Это отношение одинаково для всех веществ. Оно называется постоянной Больцмана, в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории.
Постоянная Больцмана равна
Уравнение (4.5.3) с учетом постоянной Больцмана записывается так:
Физический смысл постоянной БольцманаИсторически температура была впервые введена как термодинамическая величина, и для нее была установлена единица измерения — градус (см. § 3.2). После установления связи температуры со средней кинетической энергией молекул стало очевидным, что температуру можно определять как среднюю кинетическую энергию молекул и выражать ее в джоулях или эргах, т. е. вместо величины Т ввести величину Т* так, чтобы
Определенная таким образом температура связана с температурой, выражаемой в градусах, следующим образом:
Поэтому постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах. Зависимость давления газа от концентрации его молекул и температурыВыразив
Из формулы (4.5.6) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
|
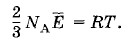
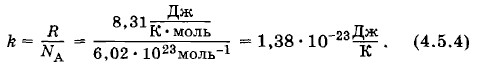
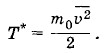
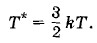
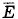из соотношения (4.5.5) и подставив в формулу (4.4.10), получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
|
|