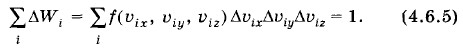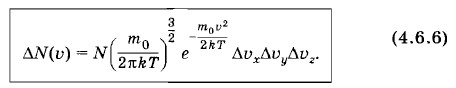|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 4. Молекулярно-кинетическая теория идеального газа § 4.6. Распределение Максвелла
Вероятность случайного событияВ § 4.1 мы уже упоминали, что для описания поведения большой совокупности молекул Дж. Максвелл ввел понятие вероятности. Как неоднократно подчеркивалось, в принципе невозможно проследить за изменением скорости (или импульса) одной молекулы на протяжении большого интервала времени. Нельзя также точно определить скорости всех молекул газа в данный момент времени. Из макроскопических условий, в которых находится газ (определенный объем и температура), не вытекают с необходимостью определенные значения скоростей молекул. Скорость молекулы можно рассматривать как случайную величину, которая в данных макроскопических условиях может принимать различные значения, подобно тому как при бросании игральной кости может выпасть любое число очков от 1 до 6 (число граней кости равно шести). Предсказать, какое число очков выпадет при данном бросании кости, нельзя. Но вероятность того, что выпадет, скажем, пять очков, поддается определению. Что же такое вероятность наступления случайного события? Пусть произведено очень большое число N испытаний (N — число бросаний кости). При этом в N' случаях имел место благоприятный исход испытаний (т. е. выпадение пятерки). Тогда вероятность данного события равна отношению числа случаев с благоприятным исходом к полному числу испытаний при условии, что это число сколько угодно велико:
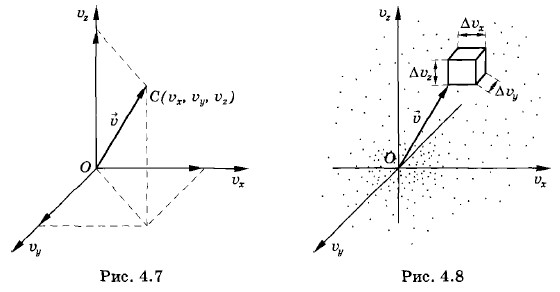
Для симметричной кости вероятность любого выбранного числа очков от 1 до 6 равна Мы видим, что на фоне множества случайных событий обнаруживается определенная количественная закономерность, появляется число. Это число — вероятность — позволяет вычислять средние значения. Так, если произвести 300 бросаний кости, то среднее число выпаданий пятерки, как это следует из формулы (4.6.1), будет равно Несомненно, что поведение молекул газа в сосуде гораздо сложнее движения брошенной игральной кости. Но и здесь можно надеяться обнаружить определенные количественные закономерности, позволяющие вычислять статистические средние, если только ставить задачу так же, как в теории игр, а не как в классической механике. Нужно отказаться от неразрешимой задачи определения точного значения скорости молекулы в данный момент и попытаться найти вероятность того, что скорость имеет определенное значение. Распределение молекул по скоростям — распределение МаксвеллаМаксвелл допустил, что в газах в состоянии теплового равновесия существует некоторое распределение скоростей, не изменяющееся с течением времени, иными словами, число молекул, имеющих скорости в заданном интервале значений, остается постоянным. И Максвелл нашел это распределение. Но главная заслуга Максвелла состояла не столько в решении этой задачи, сколько в самой постановке новой проблемы. Он ясно осознал, что случайное в данных макроскопических условиях поведение отдельных молекул подчинено определенному вероятностному, или статистическому, закону. Этот статистический закон для распределения молекул газа по скоростям оказался сравнительно простым. Наглядно распределение молекул по скоростям можно представить следующим образом. Выберем прямоугольную систему отсчета, на осях которой будем откладывать проекции υx, υy, υz скоростей частиц. В результате получится трехмерное «пространство скоростей», каждая точка которого соответствует молекуле со строго заданной скоростью Общее представление о распределении молекул по скоростям получится, если скорость каждой из N молекул изобразить точкой в этом пространстве скоростей (рис. 4.8). Точки окажутся расположенными довольно хаотически, но в среднем плотность точек будет убывать по мере удаления от начала отсчета (не все значения скоростей молекул встречаются одинаково часто). Картина распределения точек, конечно, не является застывшей. С течением времени скорости молекул за счет столкновений меняются и, следовательно, меняется картина распределения точек в пространстве скоростей. Однако ее изменение таково, что средняя плотность точек в любой области пространства скоростей со временем не будет изменяться, она остается одной и той же. Именно это и означает существование определенного статистического закона. Средней плотности соответствует наиболее вероятное распределение скоростей.
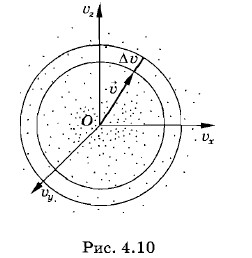
Число точек ΔN в некотором малом объеме ΔυxΔυyΔυz пространства скоростей, очевидно, равно этому объему, помноженному на плотность точек внутри него. (Аналогично масса Δm некоторого объема ΔV равна произведению плотности вещества р на этот объем: Δm = ρΔV.) Обозначим через Nƒ(υx, υy, υz) среднюю плотность точек в пространстве скоростей, т. е. число точек, приходящихся на единицу объема пространства скоростей (N — общее число молекул газа). Тогда
Фактически ΔN — это число молекул, проекции скоростей которых лежат в интервалах значений от υx до υx + Δυx, от υу до υy + Δυy и от υz до υz + Δυz (радиусы-векторы скоростей этих молекул оканчиваются внутри объема пространства скоростей Δυ = ΔυxΔυyΔυz, имеющего форму куба (см. рис. 4.8). Вероятность того, что проекции скорости молекулы лежат в заданном интервале скоростей, равна отношению числа молекул с данным значением скорости к полному числу молекул:
Функция ƒ(υx, υy, υz) называется функцией распределения молекул по скоростям и представляет собой плотность вероятности, т. е. вероятность, отнесенную к единичному объему пространства скоростей. Скорости молекул в данный момент времени в принципе могут оказаться любыми. Но вероятность различных распределений скоростей неодинакова. Среди всех возможных мгновенных распределений имеется одно, вероятность которого больше, чем всех других, — наиболее вероятное распределение. Максвелл установил, что функция распределения ƒ(υx, υy, υz), дающая это наивероятнейшее распределение скоростей молекул (распределение Максвелла), определяется отношением кинетической энергии молекулы
Здесь е ≈ 2,718 — основание натуральных логарифмов, а величина А не зависит от скорости. Таким образом, по Максвеллу, плотность точек, изображающих молекулы в пространстве скоростей, максимальна вблизи начала отсчета (υ = 0) и убывает с ростом υ, причем тем быстрее, чем меньше энергия теплового движения kT. На рисунке 4.9 представлена зависимость функции распределения ƒ от проекции υx при условии, что проекции υy и υ2 любые. Функция распределения имеет характерную колоколообразную форму, которая часто встречается в статистических теориях и называется кривой Гаусса.
Постоянную А находят из условия, что вероятность для скорости молекулы иметь любое значение от нуля до бесконечности должна равняться единице. Это условие называется условием нормировки. (Аналогично вероятность выпадания любого числа очков от 1 до 6 при данном бросании игральной кости равна единице.) Полная вероятность получается сложением вероятностей всех возможных взаимоисключающих реализаций случайного события. Суммируя вероятности ΔWi всех возможных значений скорости
Вычислив с помощью уравнения (4.6.5) нормировочную постоянную А, можно записать выражение для среднего числа частиц со скоростями в заданном интервале в следующей форме:
Скорость любой молекулы в данный момент времени — случайная величина. Поэтому и само распределение молекул по скоростям в данный момент времени случайно. Но среднее распределение, определяемое статистическим законом, реализуется с необходимостью в определенных макроскопических условиях и не меняется со временем. Однако всегда есть от клонения от средних — флуктуации. Эти отклонения с равной вероятностью происходят в ту и в другую сторону. Именно поэтому в среднем имеется определенное распределение молекул по скоростям. Распределение молекул по скоростям Максвелла оказывается справедливым не только для газов, но и для жидкостей и твердых тел. Лишь в том случае, когда для описания движения частиц нельзя применить классическую механику, распределение Максвелла перестает быть верным.
|
|
|




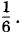 .
.
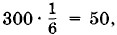 причем совершенно безразлично, бросать 300 раз одну и ту же кость или одновременно 300 одинаковых костей.
причем совершенно безразлично, бросать 300 раз одну и ту же кость или одновременно 300 одинаковых костей.
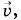 равной по модулю длине радиуса-вектора, проведенного из начала системы отсчета в эту точку (рис. 4.7).
равной по модулю длине радиуса-вектора, проведенного из начала системы отсчета в эту точку (рис. 4.7).
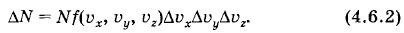
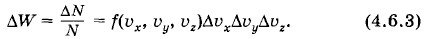
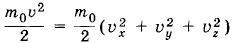 к средней энергии ее теплового движения kT (k — постоянная Больцмана). Это распределение имеет вид
к средней энергии ее теплового движения kT (k — постоянная Больцмана). Это распределение имеет вид
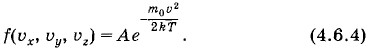
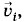 получим уравнение
получим уравнение