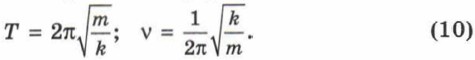Периоды колебаний пружинного и математического маятников (продолжение)

Поскольку проекция скорости υ_х является производной по времени от смещения х, получаем:

а_х = υ'_х ⇒ а_х = (x')' ⇒ а_х = x".

Итак, проекция ускорения а_х — это вторая производная от смещения х:

а_х = х". (3)

Подставляя это выражение в формулу (1), получаем:

Выясним теперь, удовлетворяет ли этому соотношению уравнение гармонических колебаний

x = x_maxcosωt. (5)

Используя формулы для производных тригонометрических функций, получаем:

х' = -ωx_maxsin ωt, (6)

х'' = -ω²x_maxcosωt. (7)

Формулу (7) можно с учётом формулы (5) записать в виде

х" = -ω²x. (8)

Эта уравнение совпадает с уравнением (4), если

Наши рассуждения опирались на то, что проекция ускорения тела прямо пропорциональна смещению тела и имеет противоположный знак. Поскольку согласно второму закону Ньютона ускорение тела прямо пропорционально равнодействующей приложенных к нему сил, мы приходим к следующему важному выводу.

Механические колебания являются гармоническими, если при отклонении тела от положения устойчивого равновесия равнодействующая приложенных к нему сил прямо пропорциональна смещению тела.

Формула (9) связывает циклическую частоту колебаний со с массой груза m и жёсткостью пружины k.

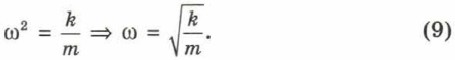
3. Объясните, почему период Т и частота ν колебаний груза на пружине выражаются формулами

период Т

4. Как надо изменить массу груза, чтобы период колебаний увеличился в 2 раза?

<<< К началу Окончание >>>