|
|
|
|
|
Глава 5. Электромагнитные волны Энергия электромагнитной волныДиаграмма направленности излученияМы рассматривали излучение заряда, движущегося прямолинейно. Интенсивность излучения оказывается зависящей от угла θ между направлением распространения излучения и направлением ускорения движущегося заряда (см. рис. 5.11).
В направлении движения (θ = 0) излучения не происходит совсем. В направлении, перпендикулярном движению Зависимость плотности потока излучения от частотыФормулы (5.5.4) и (5.5.5) для E и В, а также выражения (5.5.3) и (5.5.7) для плотности энергии и плотности потока излучения справедливы не только для ускоренного движения при торможении, но и для любого ускоренного движения. В частности, и для заряда, совершающего гармонические колебания с частотой ω. Ускорение при гармонических колебаниях пропорционально квадрату частоты колебаний. Следовательно, согласно (5.5.4) и (5.5.5) Е ~ ω2 и В ~ ω2. Поэтому плотность потока излучения пропорциональна четвертой степени частоты. При увеличении частоты колебаний всего лишь в два раза излучаемая энергия возрастает в 16 раз. Вот почему при колебаниях низкой частоты излучения практически не происходит. Так, промышленные переменные токи частотой 50 Гц практически не излучают. В антеннах передающих радиостанций приходится возбуждать колебания с частотами от десятков тысяч до десятков миллионов герц. Бегущая сферическая волнаОт заряда, совершающего гармонические колебания, распространяется сферическая волна. Амплитуда этой волны убывает как
Но в отличие от плоской волны* амплитуда напряженности электрического поля в волне убывает с расстоянием Фаза колебаний магнитной индукции совпадает с фазой колебаний напряженности
* На больших расстояниях от источника участок сферической волны размером («г можно рассматривать как участок плоской волны. Этот факт вытекает из уравнений Максвелла, но пояснить его наглядно весьма затруднительно. Суть дела в том, что скорость изменения напряженности Вблизи заряда, совершающего гармонические колебания, напряженность его кулоновского поля смещена по фазе относительно магнитной индукции
|
|
|



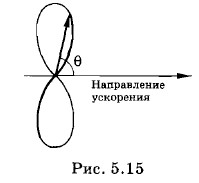
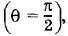 интенсивность излучения максимальна. Распределение интенсивности излучения под различными углами удобно характеризовать диаграммой направленности. Она строится так: из точки, где находится заряд, проводятся направленные отрезки, длины которых пропорциональны интенсивности излучения, т. е. sin2 θ (рис. 5.15). Получается кривая, напоминающая восьмерку. Это и есть диаграмма направленности. Подобную диаграмму направленности имеет прямолинейная антенна радиопередатчика.
интенсивность излучения максимальна. Распределение интенсивности излучения под различными углами удобно характеризовать диаграммой направленности. Она строится так: из точки, где находится заряд, проводятся направленные отрезки, длины которых пропорциональны интенсивности излучения, т. е. sin2 θ (рис. 5.15). Получается кривая, напоминающая восьмерку. Это и есть диаграмма направленности. Подобную диаграмму направленности имеет прямолинейная антенна радиопередатчика.
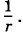 Векторы
Векторы 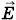 и
и 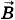 в волне перпендикулярны друг другу (см. § 5.3, в котором рассматривалась плоская волна) и составляют правый винт с направлением распространения волны. В любой точке на расстоянии г от заряда происходят гармонические колебания напряженности электрического поля и магнитной индукции. Фазы колебаний
в волне перпендикулярны друг другу (см. § 5.3, в котором рассматривалась плоская волна) и составляют правый винт с направлением распространения волны. В любой точке на расстоянии г от заряда происходят гармонические колебания напряженности электрического поля и магнитной индукции. Фазы колебаний 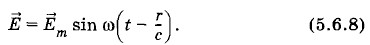
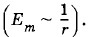
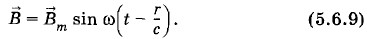
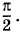 Ведь Ек - q, а В - I = q'. Вблизи заряда напряженность кулоновского поля значительно превосходит напряженность вихревого электрического поля электромагнитной волны из-за того, что выражение (5.5.4) для Ев содержит малый множитель
Ведь Ек - q, а В - I = q'. Вблизи заряда напряженность кулоновского поля значительно превосходит напряженность вихревого электрического поля электромагнитной волны из-за того, что выражение (5.5.4) для Ев содержит малый множитель 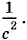 Но вдали от заряда кулоновское поле становится пренебрежимо малым по сравнению с поперечным полем волны, так как его напряженность убывает как
Но вдали от заряда кулоновское поле становится пренебрежимо малым по сравнению с поперечным полем волны, так как его напряженность убывает как 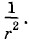 Практически остается только поперечное поле электромагнитной волны.
Практически остается только поперечное поле электромагнитной волны.