|
|
|
|
|
§ 1. Определение подобных треугольников Определение подобных треугольниковВ повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и тен- нисный мячи, круглая тарелка и боль- шое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любые два квадрата, любые два круга.
Введём понятие подобных треугольников. Пусть у двух треугольников АВС и А1В1С1 углы соответственно равны: ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1. В этом случае стороны АВ и А1В1, ВС и B1C1, СА и С1А1 называются сходственными (рис. 188).
Определение
Другими словами, два треугольника подобны, если для них можно ввести обозначения АВС и А1В1С1 так, что
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. Подобие треугольников АВС и А1В1С1 обозначается так: Оказывается, что подобие треугольников можно установить, проверив только некоторые из равенств (1) и (2). В следующем параграфе мы рассмотрим три признака подобия треугольников.
|
|
|




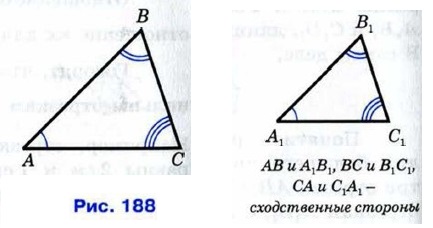
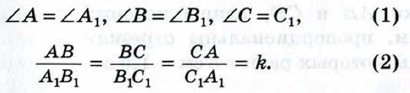
 На рисунке 188 изображены подобные треугольники.
На рисунке 188 изображены подобные треугольники.