|
|
|
|
|
§ 3. Применение подобия к доказательству теорем и решению задач Средняя линия треугольникаЗадача 2 Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. Решение Пусть
Треугольники АВС и ACD подобны по первому признаку подобия треугольников (∠A — общий, ∠ACB = ∠ADC = 90°). Точно так же подобны треугольники АВС и CBD (∠B — общий и ∠ACB = ∠BDC- 90°), поэтому ∠A = ∠BCD. Наконец, треугольники ACD и CBD также подобны по первому признаку подобия (в этих треугольниках углы с вершиной D прямые и ∠A = ∠BCD), что и требовалось доказать. Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если
Исходя из задачи 2, докажем следующие утверждения: 10. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. Действительно,
|
|
|



 АВС — прямоугольный треугольник с прямым углом С, CD — высота, проведённая из вершины С к гипотенузе АВ (рис. 197). Докажем, что
АВС — прямоугольный треугольник с прямым углом С, CD — высота, проведённая из вершины С к гипотенузе АВ (рис. 197). Докажем, что 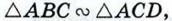
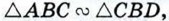
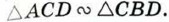
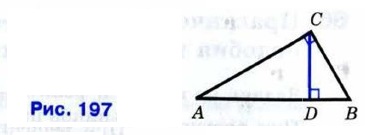
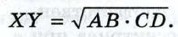
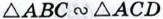 (см. рис. 197), поэтом
(см. рис. 197), поэтом 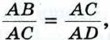 и, следовательно,
и, следовательно,