|
|
|
|
|
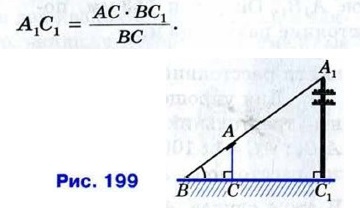
§ 3. Применение подобия к доказательству теорем и решению задач Практические приложения подобия треугольников (окончание)Измерительные работы на местностиСвойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности. Мы рассмотрим две задачи: определение высоты предмета и расстояния до недоступной точки. Определение высоты предмета. Предположим, что нам нужно определить высоту какого- нибудь предмета, например высоту телеграфного столба А1С1, изображённого на рисунке 199. Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А, столба, как показано на рисунке. Отметим на поверхности земли точку В, в которой прямая А,А пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников (∠C1 = ∠C = 90°, ∠B — общий). Из подобия треугольников следует:
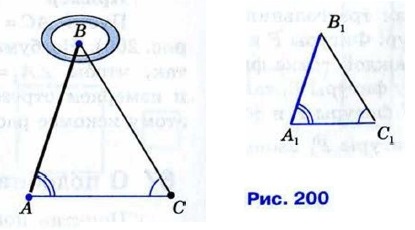
Измерив расстояния ВС1 и ВС и зная длину АС шеста, по полученной формуле определяем высоту А1С1 телеграфного столба. Если, например, ВС1 = 6,3 м, ВС = 2,1 м, АС = 1,7 м, то Определение расстояния до недоступной точки. Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В (рис. 200). Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его.
Затем с помощью астролябии измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник А1В1С1, у которого ∠A1 = ∠A, ∠C1 = ∠C, и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольники АВС и А1В1С1 подобны (по первому признаку подобия треугольников), то Для упрощения вычислений удобно построить треугольник А1В1С1 таким образом, чтобы А1С1 : АС = 1 : 1000. Например, если АС = 130 м, то расстояние А1С1 возьмём равным 130 мм. В этом случае Пример Пусть АС = 130 м, ∠A = 73°, ∠C = 58° (см. рис. 200). На бумаге строим треугольник А1В1С1 так, чтобы ∠A1 = 73°, ∠C1 = 58°, А1С1 = 130 мм, и измеряем отрезок А1В1. Он равен 153 мм, поэтому искомое расстояние равно 153 м.
|
|
|



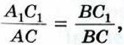 откуда
откуда
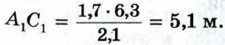
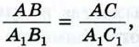 откуда получаем
откуда получаем 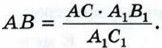 Эта формула позволяет по известным расстояниям АС, А1С1 и А1В1 найти расстояние АВ.
Эта формула позволяет по известным расстояниям АС, А1С1 и А1В1 найти расстояние АВ.
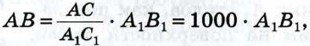 по этому, измерив расстояние А1В1 в миллиметрах, мы сразу получим расстояние АВ в метрах.
по этому, измерив расстояние А1В1 в миллиметрах, мы сразу получим расстояние АВ в метрах.