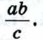|
|
|
|
|
Глава VII. Подобные треугольники Дополнительные задачи к главе VII (продолжение)615.* Отрезок с концами на боковых сторонах трапеции параллелен её основаниям и проходит через точку пересечения диагоналей. Найдите длину этого отрезка, если основания трапеции равны а и b. 616. Докажите, что вершины треугольника равноудалены от прямой, содержащей его среднюю линию. 617. Докажите, что середины сторон ромба являются вершинами прямоугольника. 618. Точки М и N являются соответственно серединами сторон CD и ВС параллелограмма ABCD. Докажите, что прямые AM и AN делят диагональ BD на три равные части. 619. 620. В треугольнике АВС (АВ≠ АС) через середину стороны ВС проведена прямая, параллельная биссектрисе угла А, которая пересекает прямые АВ и АС соответственно в точках D и Е. Докажите, что BD = CE. 621. В трапеции ABCD с основаниями AD и ВС сумма оснований равна b, диагональ АС равна a, ∠ACB = α. Найдите площадь трапеции. 622. 623. 624. Докажите, что медианы треугольника разбивают его на шесть треугольников, площади которых попарно равны. 625. 626. Докажите, что треугольники АВС и А1В1С1 подобны, если Задачи на построение627. Дан треугольник АВС. Постройте треугольник А1В1С1, подобный треугольнику АВС, площадь которого в два раза больше площади треугольника АВС. 628. Даны три отрезка, длины которых соответственно равны а, b и с. Постройте отрезок, длина которого равна 629. 630.
|
|
|



 Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке D. Докажите, что
Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке D. Докажите, что 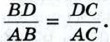
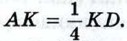 Диагональ АС и отрезок В К пересекаются в точке Р. Найдите площадь параллелограмма ABCD, если площадь треугольника АРК равна 1 см2.
Диагональ АС и отрезок В К пересекаются в точке Р. Найдите площадь параллелограмма ABCD, если площадь треугольника АРК равна 1 см2.
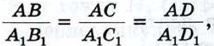 где AD и A1D1 — биссектрисы треугольников.
где AD и A1D1 — биссектрисы треугольников.