|
|
|
|
|
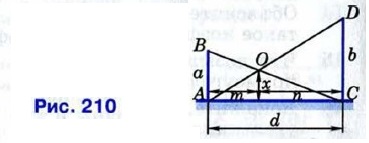
Глава VII. Подобные треугольники Дополнительные задачи к главе VII604. 605. Диагональ АС трапеции ABCD делит её на два подобных треугольника. Докажите, что АС2 = а • b, где а и b — основания трапеции. 606. 607. 608. На продолжении боковой стороны ОВ равнобедренного треугольника АО В с основанием АВ взята точка С так, что точка В лежит между точками О и С. Отрезок АС пересекает биссектрису угла АОВ в точке М. Докажите, что AM < МС. 609. На стороне ВС треугольника АВС взята точка D так, что 610. Прямая, параллельная стороне АВ треугольника АВС, делит сторону АС в отношении 2 : 7, считая от вершины А. Найдите стороны отсечённого треугольника, если АВ = 10см, ВС = 18 см, СА = 21,6 см. 611. Докажите, что медиана AM треугольника АВС делит пополам любой отрезок, параллельный стороне ВС, концы которого лежат на сторонах АВ и АС. 612. Два шеста АВ и CD разной длины а и b установлены вертикально на некотором расстоянии друг от друга так, как показано на рисунке 210. Концы А и D, В и С соединены верёвками, которые пересекаются в точке О. По данным рисунка докажите, что:
Найдите х и докажите, что х не зависит от расстояния d между шестами АВ и CD.
613. Докажите, что треугольники АВС и А1В1С1 подобны, если:
б) ∠А = ∠A1, 614.
|
|
|



 Треугольники АВС и А1В1С1 подобны, АВ = 6 см, ВС- 9 см, С А = 10 см. Наибольшая сторона треугольника А1В1С1 равна 7,5 см. Найдите две другие стороны треугольника А1В1С1.
Треугольники АВС и А1В1С1 подобны, АВ = 6 см, ВС- 9 см, С А = 10 см. Наибольшая сторона треугольника А1В1С1 равна 7,5 см. Найдите две другие стороны треугольника А1В1С1.
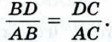 Докажите, что AD — биссектриса треугольника АВС.
Докажите, что AD — биссектриса треугольника АВС.
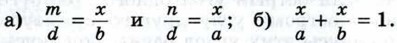
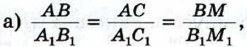 где ВМ и В1М1 — медианы треугольников;
где ВМ и В1М1 — медианы треугольников;
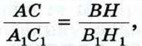 где ВН и В1Н1 — высоты треугольников АВС и A1B1C1.
где ВН и В1Н1 — высоты треугольников АВС и A1B1C1.