|
|
|
|
|
§ 1. Касательная к окружности Касательная к окружностиМы доказали, что прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. На рисунке 212 прямая р — касательная к окружности с центром О, А — точка касания. Докажем теорему о свойстве касательной к окружности. Теорема
Доказательство Пусть р — касательная к окружности с центром О, А — точка касания (см. рис. 212). Докажем, что касательная р перпендикулярна к радиусу ОА.
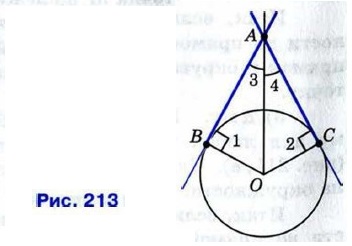
Предположим, что это не так. Тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки. Но это противоречит условию: прямая р — касательная. Таким образом, прямая р перпендикулярна к радиусу ОА. Теорема доказана. Рассмотрим две касательные к окружности с центром О, проходящие через точку А и касающиеся окружности в точках В и С (рис. 213). Отрезки АВ и АС назовём отрезками касательных, проведёнными из точки А. Они обладают следующим свойством:
|
|
|