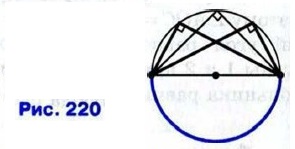
Теорема о вписанном угле (окончание)

3) Луч ВО не делит угол ABC на два угла и не совпадает со стороной этого угла. Для этого случая, пользуясь рисунком 218, в, проведите доказательство самостоятельно.

Следствие 1

Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 219).

Следствие 2

Вписанный угол, опирающийся на полуокруж ность, — прямой (рис. 220).

Используя следствие 1, докажем теорему о произведении отрезков пересекающихся хорд.

Теорема

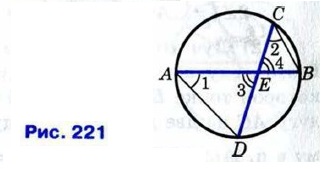
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Доказательство

Пусть хорды АВ и CD пересекаются в точке Е (рис. 221). Докажем, что

АЕ • ВЕ = СЕ • DE.

Рассмотрим треугольники ADE и СВЕ. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные. По первому признаку подобия треугольников 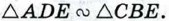Отсюда следует, что или АЕ • BE = СЕ • DE. Теорема доказана.

<<< К началу