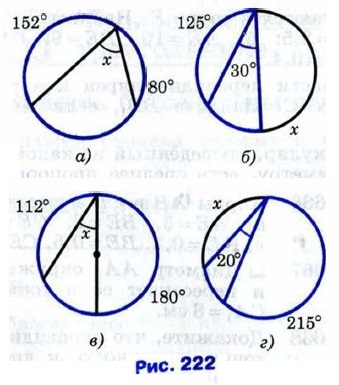
|
|
|
|
|
§ 2. Центральные и вписанные углы Задачи к § 2. Центральные и вписанные углы649. 650. 651. Хорды АВ и CD окружности с центром О равны. а) Докажите, что две дуги с концами А и В соответственно равны двум дугам с концами С и D.
652. 653. Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна: а) 48°; б) 57°; в) 90°; г) 124°; д) 180°. 654.
655. 656. Хорда АВ стягивает дугу, равную 115°, а хорда АС — дугу в 43°. Найдите угол ВАС. 657. Точки А и В разделяют окружность на две дуги, меньшая из которых равна 140°, а большая точкой М делится в отношении 6 : 5, считая от точки А. Найдите угол ВАМ. 658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая AD, проходящая через центр О (D — точка на окружности, О лежит между А и D). Найдите ∠BAD и ∠ADB, если 659. Докажите, что градусные меры дуг окружности, заключённых между параллельными хордами, равны. 660. 661. 662. 663. Отрезок АС — диаметр окружности, АВ — хорда, МА — касательная, угол МАВ острый. Докажите, что ∠MAB = ∠ACB.
|
|
|



 Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ так, чтобы: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB = 120°; г) ∠AOB = 180°.
Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ так, чтобы: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB = 120°; г) ∠AOB = 180°.
 АС = 37°,
АС = 37°,