|
|
|
|
|
§ 3. Четыре замечательные точки треугольника Свойства биссектрисы углаДокажем сначала теорему о биссектрисе угла. Теорема
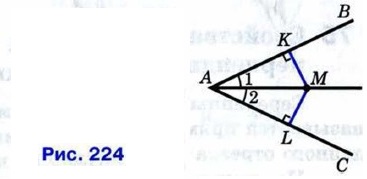
Доказательство 1) Возьмём произвольную точку М на биссектрисе угла ВАС, проведём перпендикуляры МК и ML к прямым АВ и АС и докажем, что MK = ML (рис. 224). Рассмотрим прямоугольные треугольники AM К и AML. Они равны по гипотенузе и острому углу (AM — общая гипотенуза, ∠1=∠2 по условию). Следовательно, MK = ML. 2) Пусть точка М лежит внутри угла ВАС и равноудалена от его сторон АВ и АС. Докажем, что луч AM — биссектриса угла ВАС (см. рис. 224). Проведём перпендикуляры МК и ML к прямым АВ и АС. Прямоугольные треугольники АМК и AML равны по гипотенузе и катету (AM — общая гипотенуза, МК = ML по условию). Следовательно, ∠1 = ∠2. Но это и означает, что луч AM — биссектриса угла ВАС. Теорема доказана.
Следствие 1
Следствие 2
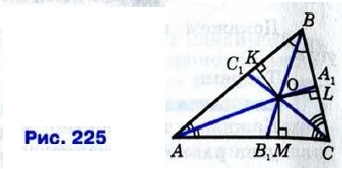
В самом деле, обозначим буквой О точку пересечения биссектрис АА1 и ВВ1 треугольника АВС и проведём из этой точки перпендикуляры OK, OL и ОМ соответственно к прямым АВ, ВС и СА (рис. 225). По доказанной теореме ОК = ОМ и OK = OL. Поэтому ОМ = OL, т. е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы треугольника АВС пересекаются в точке О, что и требовалось доказать.
|
|
|